Базис векторов.

· называются линейно зависимыми, если существуют числа l₁, l₂, …, l_n, не все равные нулю, такие, что выполняется равенство

Если равенство выполняется только для l₁=l₂=…=l_n=0, то вектора называются линейно независимыми.

Если вектора линейно зависимые, то один из них можно выразить через другие.

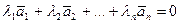, существует .

Пусть , тогда , тогда

Для двух векторов получим условие коллинеарности .

· На плоскости любые три вектора линейно зависимые, любые два коллинеарных вектора линейно независимые.

· В пространстве любые четыре вектора линейно зависимые, любые три компланарных вектора линейно независимые.

· – образуют базис, если они линейно независимые и любой вектор 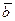единственным образом можно представить в виде (это есть разложение 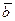по базису (), тогда – координата вектора 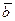в базисе (а₁, а₂, …, а_n).

Чаще всего пользуются прямоугольным базисом.

– единичные вектора (орты). Орты направлены по осям и имеют единичную длину: .

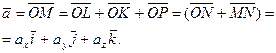
a_x, a_y, a_z – прямоугольные координаты вектора .

– разложение по ортам.

– координатная форма записи.

НАПРАВЛЯЮЩИЕ КОСИНУСЫ:

ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ:

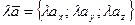
ПРИЗНАК КОЛЛИНЕАРНОСТИ ВЕКТОРОВ:

, Если вектора коллинеарны, то их одноименные координаты пропорциональны.

РАДИУС–ВЕКТОР ТОЧКИ:

М(х; у; z)

КООРДИНАТЫ ПО КООРДИНАТАМ НАЧАЛА И КОНЦА.

Итак, чтобы найти координаты вектора, нужно из координат конца вычесть координаты начала.

ДЕЛЕНИЕ ОТРЕЗКА В ЗАДАННОМ ОТНОШЕНИИ:

Найти М(x; y; z).

ЧАСТНЫЙ СЛУЧАЙ: Если М – середина АВ, то l=1 и

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.

Обозначение:

Скалярным произведением векторов называется число .

(аналогично можно получить ).

СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ:

1)

2)

3)

Доказательство:

.

4)

Доказательство:

5) ,

Скалярное произведение в координатах:

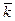
ПРИМЕНЕНИЕ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ:

1)

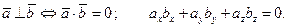
2)

3)

4) Работа постоянной силы:

ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.

Обозначение: или .

Вектора , взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора 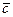кратчайший поворот от вектора к вектору 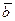виден совершающимся против часовой стрелки, иначе тройка левая.

Правая тройка:

Это тоже правая тройка:

Левая тройка:

Векторным произведением векторов и 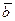называется вектор 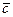,обладающий свойствами:

1) образуют правую тройку;

2) ;

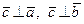3) величина вектора 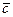численно равна площади параллелограмма, построенного на векторах и .

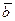СВОЙСТВА :

1) (тройка станет не левой, а правой)

2)

3)

4)

Векторное произведение в координатах:

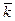
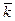
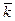
ПРИМЕНЕНИЕ :

1)

2)

ПРИМЕР:

Найти треугольника АВС, если А (4; –14; 8), В (2; –18; 12), С (12; –8; 12).

Дата добавления: 2015-10-24