Замечательные пределы.

¨ I замечательный предел:

Доказательство:

Если x < 0, то (x ~(– x)) , значит неравенство (*) выполняется для x < 0.

Перейдем в (*) к : .

¨ II замечательный предел:

Теорема: 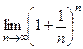существует.

Доказательство:

По теореме Вейерштрасса предел существует, если переменная величина (последовательность) ограничена и монотонна.

Бином Ньютона:

Итак, , т.е. величина ограниченная; при увеличении n количество положительных слагаемых в разложении растет, следовательно, последовательность возрастает, т.е. монотонна. Таким образом, по теореме Вейерштрасса существует предел:

Теорема (второй замечательный предел):

Доказательство:

1) Пусть x ®+¥, тогда можно найти такие целые числа, что n < x £ n + 1,

В (**) x ®+¥, тогда n ®¥

Таким образом, .

2) x ® –¥

Второй замечательный предел доказан.

ЗАМЕЧАНИЕ:

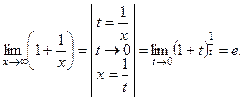
НЕПРЕРЫВНОСТЬ ФУНКЦИИ.

Определение непрерывности:

Пусть функция f(x) определена в некоторой окрестности точки x ₀ и в самой этой точке, тогда f(x) непрерывна в точке x ₀, если .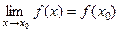

Теорема: Если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, то функция является непрерывной.

Доказательство:

Определение: x₀ называется точкой разрыва функции f(x), если в ней не выполняется условие непрерывности .

Классификация точек разрыва:

1) x ₀ Ï D(f), т.е. f(x ₀ ) не существует.

Пример: ; x = 0 – точка разрыва.

2) Не существует

Пример:

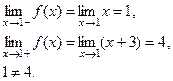
Односторонние пределы не равны, следовательно предел функции в точке не существует.

3) Существует f(x ₀ ) и существует .

Пример:

, т.е. x = 0 – точка разрыва.

Определение: Точка x = x ₀ называется точкой разрыва первого рода, если в ней существует конечные односторонние пределы A ₁ и A ₂.

h = | A ₁ – A ₂| называется скачком функции в точке x ₀.

Точка x = x ₀ называется точкой разрыва второго рода, если она не является точкой разрыва первого рода.

Дата добавления: 2015-10-24