
|
Читайте также: |
Функция называется дифференцируемой на отрезке, если она дифференцируема в каждой точке этого отрезка, т.е. в каждой точке отрезка есть производная.
Пусть u(x), v(x) – дифференцируемы на [ a, b ].
1) 
2) 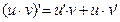
3) 
4) 
5) 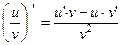
6) 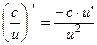
7) Производная сложной функции:

8) Производная обратной функции:
y = y(x) – дифференцируема и строго монотонна.
x = x(y) – обратная функция, тогда 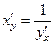 .
.
9) ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ, ЗАДАННОЙ НЕЯВНО.
F(x, y) = 0.
Пример: Найти y ¢, если 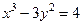 .
.
При дифференцировании учитываем, что 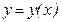 .
.
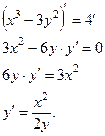
II способ:
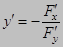
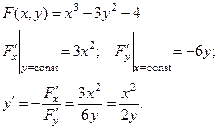
10) ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ.

Из первого уравнения получаем: t = j(x) – это обратная функции x.
Тогда 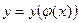 – сложная функция.
– сложная функция.
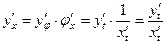
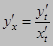
Пример:

Доказательства:
(1) 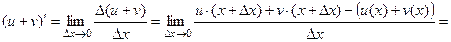
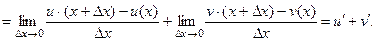
(2) 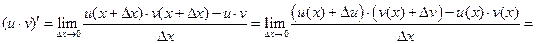
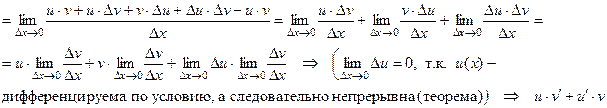
(3) 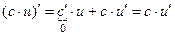
(4) 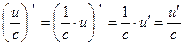
(5) доказывается так же, как (2)
(6) выводится из (5)
(7) 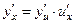
по условию y(u) и u(x) – дифференцируемы;
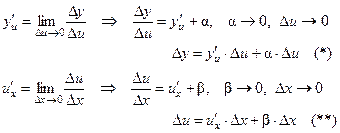
Подставим (**) в (*), получим:
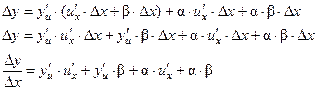

(8) 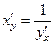
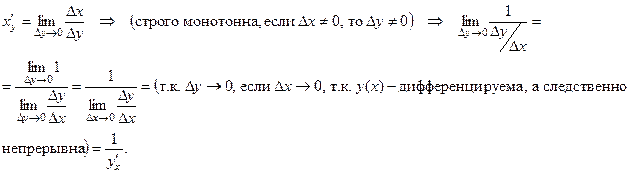
ТАБЛИЦА ПРОИЗВОДНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ.
1) 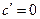
| 10) 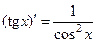
|
2) 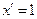
| 11) 
|
3) 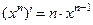
| 12) 
|
3.1) 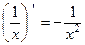
| 13) 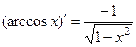
|
3.2) 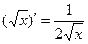
| 14) 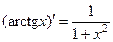
|
4) 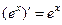
| 15) 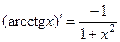
|
5) 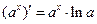
| 16) 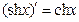
|
6) 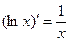
| 17) 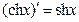
|
7) 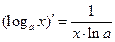
| 18) 
|
8) 
| 19) 
|
9) 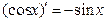
|
Доказательства:
(1) смотри пример выше.
(2) самостоятельно (это частный случай (3))
(3) 
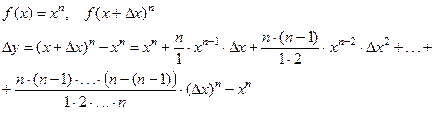
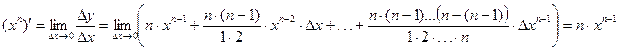 – доказательство для натуральных n, для рациональных докажем позже.
– доказательство для натуральных n, для рациональных докажем позже.
(3.1) и (3.2) самостоятельно.
(4) 
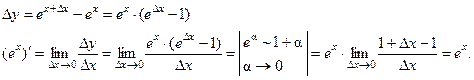
(5) 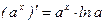

(6) 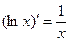

(7) 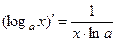

(8) 
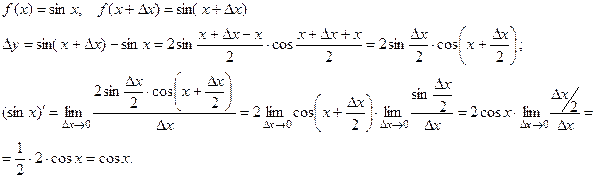
(9) 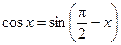
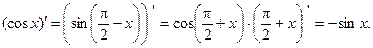
(10) 
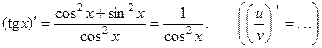
(11) 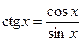 – аналогично (10).
– аналогично (10).
(12) 
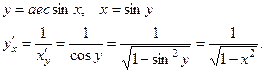
(13), (14) и (15) – аналогично.
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ.
 1) 1) 
| |
 2) 2) 
| |
 3) 3) 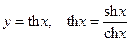
| |
 4) 4) 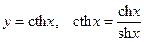
|
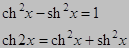
(16) – (19) – по определению.
Например,
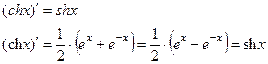
ТАБЛИЦА ПРОИЗВОДНЫХ СЛОЖНЫХ ФУНКЦИЙ.
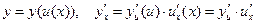
1) 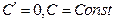 , ,
| 10) 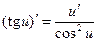
|
2) 
| 11) 
|
3) 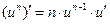
| 12) 
|
3.1) 
| 13) 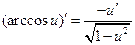
|
3.2) 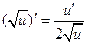
| 14) 
|
4) 
| 15) 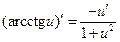
|
5) 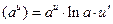
| 16) 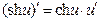
|
6) 
| 17) 
|
7) 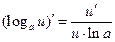
| 18) 
|
8) 
| 19) 
|
9) 
|
ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ.
Сначала функцию логарифмируют, потом дифференцируют. Этот прием удобно применять, когда функция является произведением или частным степенных функций, или является показательно-степенной функцией.
Пример:

Пример:
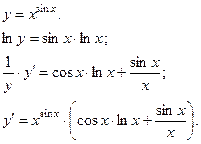
Пример:
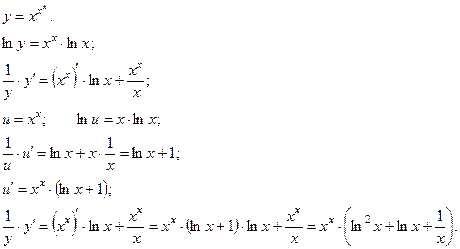
ДИФФЕРЕНЦИАЛ ФУНКЦИИ.

Умножим это выражение на D x:

Определение: Главная часть приращения функции, равная 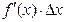 называется дифференциалом
называется дифференциалом 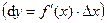 .
.
Замечание: 1) 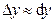
2) 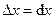
Доказательство:
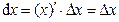
Пример: Найти d y, если 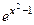 , x изменяется от x = 1 до x = 0,9.
, x изменяется от x = 1 до x = 0,9.
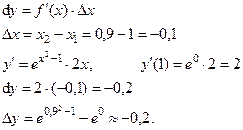
 ГЕОМЕТРИЧЕСКИЙ СМЫСЛ d y.
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ d y.
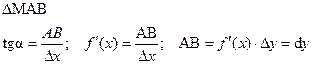
Дифференциал в точке равен приращению ординаты касательной, проведенной в этой точке.
Пример: вычислить приближенно  .
.
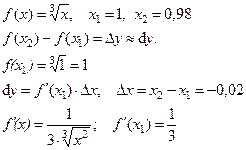
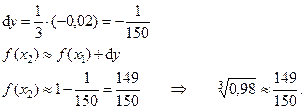
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ.
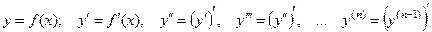
Начиная с четвертой производной пишут: 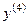 или
или 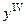 .
.
ВТОРАЯ ПРОИЗВОДНАЯ НЕЯВНО ЗАДАННОЙ ФУНКЦИИ.

Пример: 

ВТОРАЯ ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ.

Пример:
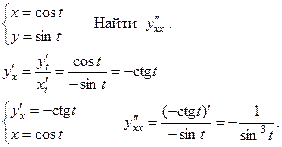
Дата добавления: 2015-10-24; просмотров: 121 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ. | | | ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ. |