
|
Читайте также: |
Пусть даны две плоскости P и Q и с.к. x1Ox2 и y1Oy2, в которой соответственно.
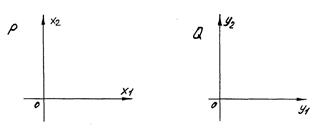
P и Q, и их с.к. могут совмещаться. Рассмотрим систему:  (1)
(1)
Из (1)  каждой точке М(x1;x2) плоск. x1Ox2 соответствует точка
каждой точке М(x1;x2) плоск. x1Ox2 соответствует точка  (y1;y2) плоск. y1Oy2. Уравнение (1)-линейное преобразование координат, отображающая плоскость x1Ox2 на плоскость y1Oy2.
(y1;y2) плоск. y1Oy2. Уравнение (1)-линейное преобразование координат, отображающая плоскость x1Ox2 на плоскость y1Oy2.
Уравнение (1)-линейное значит и отображение линейное.
Если рассмотреть некоторую область F в плоскости x1Ox2, то с помощью уравнений (1) ей будет соответствовать некоторая совокупность точек  плоскости y1Oy2.
плоскости y1Oy2.

В общем случае можно записать (не линейное отображение): 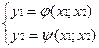
Отображение (1) полностью определяется совокупностью коэффициентов a11,a12,a21,a22.
Прямоугольная таблица из mn элементов, содержащая m строк и n столбцов,А=  или А=
или А=  или А=
или А=  наз. матрицей, где a11, a12, a13 …, amn -элементы матрицы, короткая запись А=(aij) или А=
наз. матрицей, где a11, a12, a13 …, amn -элементы матрицы, короткая запись А=(aij) или А=  или А=[aij], где i-номер строки, j-номер столбца, i=1, 2…, m=
или А=[aij], где i-номер строки, j-номер столбца, i=1, 2…, m=  ; j=1,2,…, n=
; j=1,2,…, n= 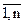 . aij – элементы (члены) матрицы.
. aij – элементы (члены) матрицы.
Прямоугольная таблица составленная из коэффициентов системы (1)  наз.матрицей отображения (1).
наз.матрицей отображения (1).
Виды матриц: квадратная, ступенчатая (треугольная), транспонированная, столбцевая, строчечная. Квадратные матрицы бывают: симметричными, диагональными, единичными.
| Итак,матрицей порядка m´n называется прямоугольная таблица чисел (элементов), содержащая m строк и n столбцов. | 
| аij – элемент матрицы а11, а22, … – эти элементы образуют главную диагональ матрицы |
1. ОСНОВНЫЕ ВИДЫ МАТРИЦ:
| 1. Квадратная – это матрица, у которой число строк равно числу столбцов (m=n). |  –2-го порядка –2-го порядка
|  –3-го порядка –3-го порядка
| ||||
| 2. Диагональная – это квадратная матрица, все элементы которой, кроме элементов главной диагонали, равны нулю. | 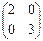 ; ;
| |||||
3.
| Е2´2= 
| 
| ||||
4.  
| 
| 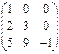
| ||||
5.  Симметрическая – это квадратная матрица, элементы которой симметричны относительно главной диагонали Симметрическая – это квадратная матрица, элементы которой симметричны относительно главной диагонали
| 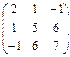
| |||||
6.
| 
| |||||
Рассмотрим матрицу состоящую из одного столбца или одной строки:
Х=  , У=
, У=  . Первая матрица называется столбцевой, вторая строчечной.
. Первая матрица называется столбцевой, вторая строчечной.
Иногда столбцевую (строчечную) матрицу отождествляют с вектором в пространстве соответственного числа измерений, где элементы матрицы являются проекциями вектора на соответствующие оси координат.
Пример.  =x1
=x1  +x2
+x2 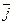 +x3
+x3  .
.
|  –вектор-строка –вектор-строка
| 
|
Две матрицы А и В равны, если они имеют одинаковое количество строк и солбцов и соответствующие их элементы равны, т.е А=В или (аij)=(bij), если aij=bij, i=  , j=
, j=  .
.
Суммой двух матриц (aij) и (bij) с одинаковым количеством строк и одинаковым количеством столбцов наз. матрицей (сij), у которой элементом сij является сумма аij и bij соответствующих элементов матриц (aij) и (bij) т.е. (aij)+(bij)=(cij)=> aij+bij=cij (i=  ; j=
; j=  ).
).
Пр.  +
+ 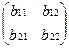 =
=  . Аналогично разность двух матриц.
. Аналогично разность двух матриц.
Чтобы умножить матрицу на число λ нужно умножить на это число каждый элемент матрицы: λ(aij)=(λaij).
Пример: λ  =
= 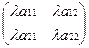 .
.
Произведением строки из n элементов (a1,a2,…,an) на столбец из n элементов  называется число (элемент) равное сумме произведений соответствующих элементов.
называется число (элемент) равное сумме произведений соответствующих элементов.

 =
=  .
.
Пример. 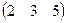
 =
=  =(32).
=(32).

 =?–неопределенно!
=?–неопределенно!
Произведением матриц  и
и  называется матрица
называется матрица  , каждый элемент которой cij равен произведению i -й строки матрицы А и j -го столбца матрицы В, т.е. (i,A и j,B).
, каждый элемент которой cij равен произведению i -й строки матрицы А и j -го столбца матрицы В, т.е. (i,A и j,B).
Пример. 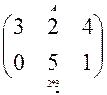  = = 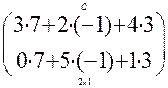 = =  .
A*B= .
A*B=   = =  = =  =Д1
B*A= =Д1
B*A=  * *  = =  = =  =Д2
Д1 =Д2
Д1  Д2 => умножение матрицы не коммутативно: АВ Д2 => умножение матрицы не коммутативно: АВ  ВА. ВА.
| ||||||||
| Итак, А = (аij); B = (bij); C = (cij). 1. СЛОЖЕНИЕ (складывать можно только матрицы одинаковой размерности): Am´n + Bm´n = Cm´n, если cij = aij + bij. |  Вычитание аналогично!
Вычитание аналогично!
| |||||||
| 2. УМНОЖЕНИЕ НА ЧИСЛО (k): k×Am´n = Bm´n, если bij = k×aij | 
| |||||||
| Матрица (–А) называется противоположной матрице А. | ||||||||
| Свойства линейных операций: 1. А+В=В+А 2. А+(В+С)=(А+В)+С 3. А–А=О (О – нулевая матрица) | 4. А+О=А 5. a(А+В)=aА+aВ 6.(a+b)А=aА+bА 7. 1×А=А | |||||||
| 3. УМНОЖЕНИЕ МАТРИЦ (строка на столбец): | ||||||||
| Am´n×Bn´p=Cm´p, если cij=ai1×b1j+ai2×b2j+…+ain×bnj. Элемент матрицы произведения, стоящий на пересечении i-той строки и j-того столбца, равен сумме произведений элементов i-той строки первой матрицы на элементы j-того столбца второй матрицы. | ||||||||

| 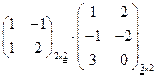
| |||||||
| Матрицы А и В называются перестановочными, если АВ=ВА. | ||||||||
| Свойства произведения матриц: 1. (А×В)×С=А×(В×С) 2. (А+В)×С=АС+ВС | 3. С×(А+В)=СА+СВ 4. А×Е=Е×А=А 5. (aА)В=А(aВ) | |||||||
| 4. ТРАНСПОНИРОВАНИЕ (АТ): Чтобы получить транспонированную матрицу, нужно в исходной матрице заменить строки на соответствующие столбцы. | ||||||||

| ||||||||
| Свойства транспонирования: | 1. (А+В)Т=АТ+ВТ | 2. (АВ)Т=ВТАТ (!) | ||||||
| 5. ВОЗВЕДЕНИЕ В СТЕПЕНЬ (только для квадратной матрицы): | ||||||||
| А2=А×А; | А3=А2×А; | Аn=Аn-1×А; | ||||||
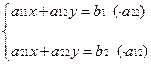 потом вычтем из первого второе, вынося х получим:
потом вычтем из первого второе, вынося х получим:  ;
Аналогично, ;
Аналогично,  .
Разности, стоящие в числителе и знаменателе a11·a22-a21·a12= .
Разности, стоящие в числителе и знаменателе a11·a22-a21·a12=  , b1a22-b2a12= , b1a22-b2a12=  и т.д. называются определителями 2-го порядка.
Вообще, определителем 2-го порядка называется число (элемент) соответствующий квадратной таблице из 4-х чисел (элементов). Определителем 3-го порядка называется число (элемент) соответствующий квадратной таблице из 9-ти чисел (элементов). и т.д. называются определителями 2-го порядка.
Вообще, определителем 2-го порядка называется число (элемент) соответствующий квадратной таблице из 4-х чисел (элементов). Определителем 3-го порядка называется число (элемент) соответствующий квадратной таблице из 9-ти чисел (элементов).
| ||
Каждой квадратной матрице соответствует число, называемое определителем матрицы. (ïАï, DА, detA, D)
Определитель составленный из элементов квадратной матрицы (без перестановок), называется определителем матрицы. Обозначение:  .
Замечание: неквадратная матрица определителя не имеет. .
Замечание: неквадратная матрица определителя не имеет.
| ||
| · det 2-го порядка называется число а11а22 – главная диагональ а12а21 – побочная диагональ | 
| |
| ||
| ПРАВИЛА ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ ТРЕТЬЕГО ПОРЯДКА: | ||
   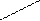             1. Правило треугольников:
1. Правило треугольников:

|
2. Правило Саррюса:
       = =  
| |
СВОЙСТВА:
1. Определитель не изменится, если его строки заменить на столбцы (detAT=detA).
2. При перестановке двух параллельных строк или столбцов определитель меняет знак.
3. Общий множитель строки или столбца можно выносить за знак определителя.
4. Определитель, имеющий две одинаковые строки или столбца, равен нулю.
СЛЕДСТВИЕ: Определитель, имеющий две пропорциональные строки или столбца, равен нулю.
5. Определитель, строка или столбец которого является суммой двух чисел, можно разложить на сумму двух определителей.

| ||
Определитель не изменится, если к элементам некоторой строки или столбца прибавить элементы другой строки или столбца, помноженные на некоторое число, не равное 0. СЛЕДСТВИЕ: Определитель, имеющий нулевую строчку или столбец, равен нулю. Чтобы сформулировать следующее свойство, введем определения: 1. Мij (минором) элемента aij определителя n-го порядка называется определитель (n-1)-го порядка, полученный из исходного вычеркиванием i-той строки и j-того столбца.
2. Алгебраическим дополнением Аij элемента aij называется Aij=(–1)i+jMij. | ||
7. Разложение определителя по строке или столбцу:
Определитель равен сумме произведений элементов некоторой строки или столбца на их алгебраические дополнения.
D=ai1Ai1+ai2Ai2+…+ainAin.
8. Сумма произведений элементов некоторой строки или столбца на алгебраическое дополнение параллельной строки или столбца равна нулю.
 , то a11A31+a12A32+a13A33=0. , то a11A31+a12A32+a13A33=0.
| ||
При помощи свойств определителя вычисление определителя любого порядка можно свести к вычислению определителя второго или третьего порядка.
Дата добавления: 2015-10-24; просмотров: 129 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА ЗАПИСИ КОМПЛЕКСНОГО ЧИСЛА. | | | СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ (СЛУ). |