Взаимное расположение двух прямых.

ПЕРЕСЕЧЕНИЕ ДВУХ ПРЯМЫХ.

Система имеет единственное решение:

УГОЛ МЕЖДУ ПРЯМЫМИ.

ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ.

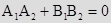
Пример: Написать уравнение прямой, проходящей через точку A (2; –1) перпендикулярно 3 x + 2 y – 4 = 0.

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ.

Пример:

– стороны параллелограмма;

M (3; –1) – точка пересечения диагоналей.

Написать уравнение двух других сторон.

Решение:

1) Находим точку B:

2) M – середина BD,

3) (DC)||(AB),

4) (AD)||(BC),

СОВПАДАЮЩИЕ ПРЯМЫЕ.

– это и есть условие совпадения двух прямых.

РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ.

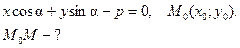
Отклонением d точки от прямой называется длина перпендикуляра, опущенного из этой точки на прямую, взятого со знаком «+», если точка и начало координат лежат по разные стороны от прямой, и со знаком «–», если по одну сторону.

– расстояние.

.

Найдем скалярное произведение, для этого надо определить значение .

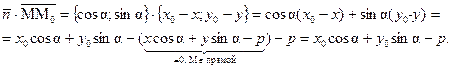
– отклонение точки M (x ₀; y ₀) от прямой,

r = |d|.

Пример: Найти расстояние между двумя параллельными прямыми

ПЛОСКОСТЬ В ПРОСТРАНСТВЕ.

НОРМАЛЬНОЕ УРАВНЕНИЕ ПЛОСКОСТИ.

– точка плоскости.

– нормальное уравнение плоскости в векторной форме.

– нормальное уравнение плоскости в координатной форме.

1) ;

2) .

Рассмотрим уравнение вида

– тоже перпендикуляр, т.е. нормаль-вектор.

– общее уравнение плоскости, .

Любое линейное уравнение задает плоскость, любая плоскость задается линейным уравнением.

Частные случаи общего уравнения:

1) – проходит через О(0; 0; 0).

2) – параллельно OZ.

3) – параллельно OY.

4) – параллельно OX.

5) – проходит через OZ.

6) – проходит через OY.

7) – проходит через OX.

8) – параллельно плоскости XOY.

– параллельно плоскости XOZ.

– параллельно плоскости YOZ.

9) – плоскость XOY; – плоскость YOZ; – плоскость XOZ.

Уравнение плоскости в отрезках.

– уравнение плоскости в отрезках.

x	a			a, b, c – отрезки на осях
y		b
z			c

Пример:

У равнение плоскости, проходящей через данную точку M (x₀;y₀;z₀).

– произвольная точка.

– нужное уравнение.

Уравнение плоскости, проходящей через три точки.

Дата добавления: 2015-10-24