Тригонометрическая форма записи комплексного числа.

Длина вектора, изображающего комплексное число , называется модулем комплексного числа.

Угол j, образуемый этим векторром с положительным направлением действительной оси (<MON), называется аргументом комплексного числа.

Обозначение: модуль ,

аргумент .

Из прямоугольного треугольника OMN

.

В качестве главного значения аргумента комплексного числа обычно выбирают значение , определенное неравенствами

,

.

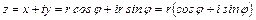Итак, называется тригонометрической формой записи комплексногочисла.

Пример. Записать в тригонометрической форме комплексные числа:

1.

2.

3.

4. .

Решение:

1.

.

2. .

.

3.

.

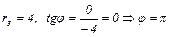
4.

.

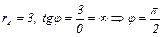
ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ.

Сложение.

Суммой двух комплексных чисел и называется комплексное число , определяемое равенством

.

Из определения вытекают следующие законы сложения:

- Переместительный:

- Сочетательный:

Вычитание.

Вычитание комплексных чисел определяется как действие, обратное сложению. Вычесть из числа число значит найти такое число 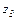, чтобы имело место равенств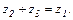о: Число 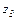называется разностью чисел 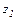и 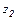и обозначается .

Вычитание всегда выполнимо.

Умножение.

Произведением двух комплексных чисел и называется комплексное число, определяемое равенством .

Из определения следуют законы:

· Переместительный

· Сочетательный

· Распределительный .

Деление.

Деление – действие, обратное умножению. Разделить комплексное число на комплексное число значит найти такое число , чтобы имело место равенство .

Тогда получаем систему для определения 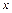и :

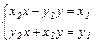
Система всегда разрешима, т.к. определитель

.

Число называется частным.

.

Итак, чтобы разделить одно комплексное число на другое, надо числитель и знаменатель дроби умножить на комплексное число, сопряженное числу, стоящему в знаменателе.

Пример.

Выполнить все действия над комплексными числами и .

Решение

Дата добавления: 2015-10-24