Ранг матрицы.

Рассмотрим матрицу общего вида (порядка m ´ n):

Минором матрицы k -того порядка называется определитель, составленный из элементов матрицы, стоящих на пересечении произвольно выбранных k строк и k столбцов.

Пример:

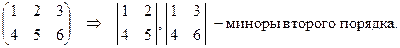
Рангом матрицы называется наивысший из порядков миноров, отличных от нуля.

Минор, порядок которого определяет ранг матрицы, называется базисным.

Пример:

Максимально возможный порядок ненулевого минора – третий, но в данном случае все миноры третьего порядка- нулевые.

Рассмотрим миноры второго порядка

Вывод: базисных миноров может быть несколько!

Для вычисления ранга матрицы можно применять метод окаймляющих миноров и метод элементарных преобразований.

Метод окаймляющих миноров заключается в нахождении ненулевого минора первого порядка, затем – ненулевого минора второго порядка, окаймляющего найденный минор первого порядка и т.д. Если на некотором шаге не удается найти ненулевой минор, то ранг равен порядку последнего найденного ненулевого минора.

Пример: найти ранг матрицы .

1) 1– минор первого порядка, 1¹0, следовательно, .

2) Окаймляют 1 миноры:

3) Окаймляющие миноры для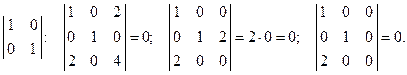

Ненулевых миноров нет, значит .

Свойства ранга матрицы:

1) Ранг не изменится, если строки заменить на столбцы ().

2) Ранг не изменится, если вычеркнуть нулевую строку или нулевой столбец.

3) Ранг не изменится при элементарных преобразованиях:

а) умножение на число отличное от нуля строки или столбца;

б) сложение и вычитание строк.

Канонической называется матрица, в начале главной диагонали которой стоят единицы, а остальные элементы равны нулю.

Матрицы называются эквивалентными (A ~ B), если одну можно получить из другой с помощью элементарных преобразований.

Метод элементарных преобразований для вычисления рангов:

Рангом конеч. сист. вект. наз. число векторов в любом ее базисе.

* Строчечным рангом матрицы наз. ранг сист. ее строк, рассм. как n-мерн. вектор.

* Столбцовым рангом матрицы наз.ранг сист. ее столбцов, рассм. m-мерн. вектор.

Теорема. Строчечный ранг ступенчат. матрицы равен числу ее ненулевых строк.

Теорема. Строчечный ранг матрицы равен ее столбцовому рангу, т.е. r(A)=ρ(A).

Схема вычисления ранга матрицы:

1. привести матрицу к ступенчатому виду;

2. сосчитать число ненулевых строк ступенчатой матрицы.

Замечание: т.к. строчечный ранг равен столбцовому, то можно говорить «ранг матрицы».

1)

2) 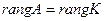и равен числу единиц в K.

Пример:

СЛУ с n-переменными x₁,x₂,…,x_n R называется система вида:

(1),

где α_ij R; β_i R; i,j N, i= ; j= .

Решением СЛУ (1) наз. арифметический n-мерный вектор (кси) ξ=(ξ₁; ξ₂; …; ξ_n), при подстановке которого вместо переменных получим все верные равенства

(1^/)

Если СЛУ (1^/) имеет хотя бы одно решение, то она называется совместной.

Если СЛУ (1) не имеет не одного решения, то будет считаться несовместной.

СЛУ (2):

называется следствием СЛУ (1), если каждое решение СЛУ (1) является решением СЛУ (2).

Рассмотрим СЛУ (1), умножим почленно каждое уравнение соответственно на
λ₁, …,λ_m R и затем почленно сложим все уравнения системы, тогда получим уравнение: (λ₁α₁₁+λ₂α₂₁+…+λ_mα_m1)x₁+(λ₁α₁₂+…+λ_mα_m2)x₂+…+(λ₁α_1n+…+λ_mα_mn)x_n=λ₁β₁+…+λ_mβ_m (3).

Линейной комбинацией СЛУ (1) называется уравнения вида (3).

Рассмотрим совокупность векторов …, (1) и возьмем совокупность чисел , ,…, (2) и (3).

Вектор называется линейной комбинацией векторов из (1).

Пусть дана линейная комбинация (4).

Совокупность векторов (1) называется линейно независимой, если в линейной комбинации (4) все коэффициенты и других не существует, т. е.

Совокупность векторов (1) называется линейно зависимой, если в линейной комбинации (4) хотя бы одно из чисел .

Теорема (без доказательства). Линейной комбинацией линейных уравнений (1) является следствием системы (1).

СЛУ (1) и (2) с переменными x₁,x₂,…,x_n наз. равносильными, если каждое решение одной системы является решением другой.

Теорема (без доказательства). СЛУ (1) и (2) будут равносильны тогда и только тогда, когда (ттт,к) каждая СЛУ является следствием другой системы.

Теорема (без доказательства). СЛУ (1) и (2) будут равносильны ттт,к множество решений одной системы и другой системы совпадают.

Пример: (А)

23x=23

X=1

3y=17-2*1

3y=15

y=5.

ξ’=(x;y)

ξ=(1;5)-решение системы А.

Множество М₁={ξ’}={(1;5)}-множество решений системы (А).

2x=2

x=1;

y=6-1

y=5

μ’=(x;y), μ’={1;5}, M₂={(1;5)}.

M₁=M₂, поэтому система А равносильна системе В.

Элементарными преобразованиями СЛУ (1) называются следующие преобразования:

1) умножение (почленное) любого уравнения на λ 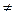0.

2) к любому уравнению системы можно прибавить другие уравнения этой системы умноженные на λ 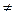0. (1 и 2 - это неособенные элементарные преобразования).

3) удаление (добавление) из системы уравнения с нулевыми коэффициентами (все нулевые). (3-это особое элементарное преобразование).

Теорема (без доказательства). Если СЛУ (2) полученное из СЛУ (1) при помощи цепочки элементарных преобразований, то эти системы равносильны.

Следствие 1. Если в СЛУ (1) уравнение заменить линейной комбинацией других уравнений этой системы, то получим систему равносильную данной.

Следствие 2. Можно добавить (удалить) уравнение я/я линейной комбинацией других уравнений этой системы, получится система равносильная данной.

Следствие 3. Если к уравнению прибавить линейную комбинацию других уравнений той-же системы, то получим систему равносильн. данной. Систему (1) можно записать еще в другом виде: в векторной и матричной форме.

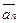= , …, = , = (1^*).

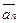Запишем равенство: x₁ +x₂ + … +x_n = (1 вект.).

Векторной формой записи СЛУ(1) наз. запись вида (1 вект.), где векторные столбцы определены равенствами (1^*)

Если в СЛУ (1) в правой части все β=0, то система наз. однородной СЛУ, если хотя бы одно β 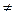0, то неоднородной.

Однородная СЛУ всегда совместна, т. к. (0, 0, …, 0).

Ненулевые решения, то есть не тривиальные решения будут:

1) ттт,к. векторы-столбцы ,будут линейно зависимы.

2) если число уравнений меньше числа переменных.

3) если ранг с. в. .

Рассмотрим условие при котором СЛУ совместна.

Дата добавления: 2015-10-24