Исследование систем на совместность.

1. Если матрица А (основная), В (расширенная), А - нулевая, В - нулевая, то СЛУ совместна и имеет большое множество решений.

2. Если А - нулевая, В - не нулевая => СЛУ не совместна => решений нет.

3. А – не нулевая, В – не нулевая. r(А) 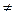r(В), то несовм. => не равно 0; если r(А) = r(В), то система совместна, при r(А) = n - одно решение, а при r(А)<n, то б.м.р.

В случае б.м.р. выберем любые n - r свободные переменные и выразим главные через n-r. Если есть решение, то его можно находить разными способами.

Изучим метод последовательного исключения переменных (метод Жордана - Гаусса):

Рассмотрим СЛУ (1): 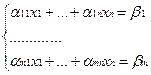пусть 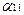- ведущий элемент (если α₁₁=0,
то найдем в первом столбце не нулевой элемент и переставим его). Если весь первый столбец нулевой, то возьмем α₁₂ и повторим. α₁₁ 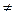0 => 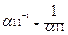(если это числа). Исключим из системы переменных Х₁ начиная со второго уравнения, для этого будем умножать первое уравнение почленно на множитель и прибавлять ко второму уравнению и так далее. Для каждого уравнения свой множитель.

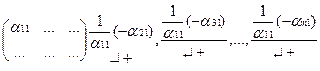
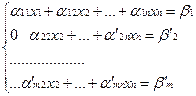Пусть теперь α^/₂₂ – ведущий элемент, т. е. α^/₂₂ 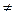0. Исключим переменную x₂ начиная с третьего уравнения. И т. д. после (s-1) шага мы придем к системе вида (обозначим α^/ – штрихи через а):

(1^**) Если s=m, то нулевых строк нет.

В зависимости от числа переменных n могут получиться:

1. форма трапеции:

2. форма треугольника.

т. о. мы приходим к выводу:

Теорема: Если СЛУ совместна, то при помощи цепочки элементарных преобразований ее можно привести к системе вида (1^**) с ненулевыми ведущими элементами. В противном случае (т. е. если не совместно) в результате преобразований получиться противоречивое равенство: 0*Х₁+…+0*Х_n=b, b 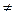0.

Заметим: что решая методом Гаусса можно вести запись системы каждый раз через равносильность, но лучше пользоваться матрицами и вести запись с помощью расширенной матрицы.

Итак, Теорема Кронекера-Капелли. Система совместна тогда и только тогда, когда ранг ее расширенной матрицы равен рангу основной матрицы системы: .

Теорема 1: Если ранг совместной системы равен числу неизвестных, то система – определенная.

Теорема 2: Если ранг совместной системы меньше числа неизвестных, то система неопределенная.

Чтобы решить систему общего вида необходимо:

1) проверить ее на совместность ();

2) Пусть 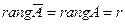, тогда

необходимо выбрать r уравнений, коэффициенты которых входят в базисный минор; остальные уравнения отбросить. Переменные, коэффициенты которых входят в базисный минор, оставить слева, остальные перенести вправо. (r переменных слева – главные, переменные справа – свободные)

3) Выразить главные переменные через свободные.

Полученное решение является общим решением системы.

Пример: Исследовать систему на совместность и найти общее решение, и одно частное решение.

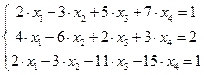
Решение:

1. Исследуем систему на совместность:

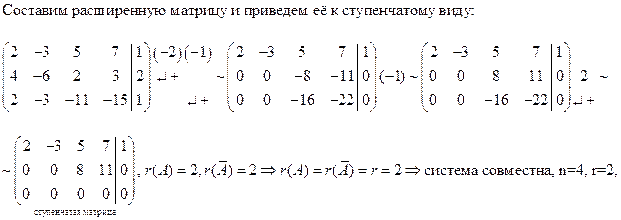
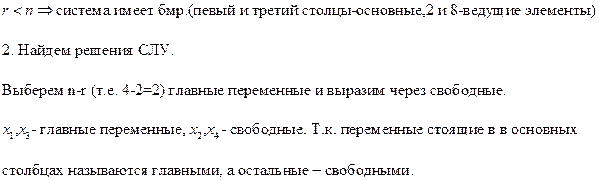
Составим систему по ступенчатой матрице:

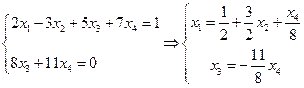
Проверка:

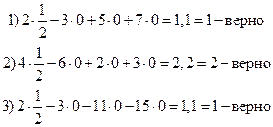
Дата добавления: 2015-10-24