Элементы дифференциального исчисления функции двух переменных.

Если каждой паре двух независимых переменных (x, y) соответствует единственное значение z, то z = z(x, y) называется функцией двух переменных.

Пример: найти D(z), если .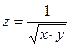

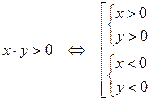
Графиком функции двух переменных является поверхность.

Пример: ,

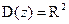
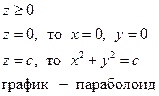
– частное приращение по x.

– частное приращение по y.

– полное приращение функции z.

Пример: найти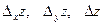

· Частной производной функции z по переменной x называется .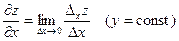

· Частной производной функции z по переменной y называется .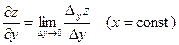

Пример: найти .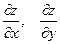

.

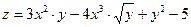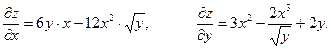
ЧАСТНЫЕ ПРОИЗВОДНЫЕ ВТОРОГО ПОРЯДКА.

Утверждение: Если смешанные частные производные непрерывны в точке, то они равны в этой точке.

Пример: 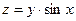, найти частные производные второго порядка.

ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ.

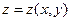
Частные дифференциалы по x и y получаются, если фиксировать одну из переменных.

Полное приращение функции:

1) 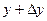– фиксирована.

По теореме Лагранжа:

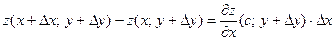
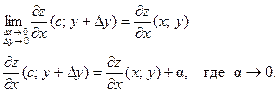
(1) .

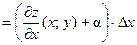2) x – фиксирован, аналогично получаем:

(2)

Первые два слагаемых главная часть приращения.

Последние два – бесконечно малые более высокого порядка, чем первые два.

Главная часть полного приращения функции двух аргументов называется полным дифференциалом.

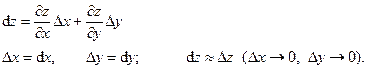
Пример: Найти .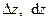

Понятие полного дифференциала полностью аналогично дифференциалу одной переменной.

ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ.

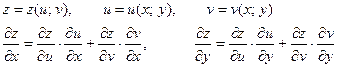
Пример:

Продифференцируем непосредственно:

По теореме:

Пример: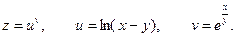

ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ НЕЯВНО.

Если частные производные в некоторой области непрерывны и в этой области, то .

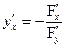Доказательство:

– данное уравнение задает кривую на плоскости. Возьмем точку 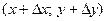на этой кривой: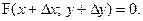

Разделим все это выражение на D x:

Пример: .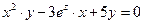

Список литературы

Основная литература:

1. Н.С. Пискунов. Дифференциальное и интегральное исчисление для втузов, в 2-х томах: Учебное пособие для втузов. – М.: Наука, 1985.

2. Д.В. Беклемишев. Курс аналитической геометрии и линейной алгебры: Учебное пособие для студентов втузов. – М.: Наука, 1980.

3. В.Е. Гмурман. Теория вероятностей и математическая статистика: Учебное пособие для вузов. – М.: Высшая школа, 1999.

4. И.Г. Араманович, Г.Л. Лунц и др. Функции комплексного переменного. Операционное исчисление. Теория устойчивости: Учебное пособие для втузов. – М.: Наука, 1978.

5. С.В. Яблонский. Введение в дискретную математику. – М.: Наука, 1986.

6. А.Н. Тихонов, А.А. Самарский. Уравнения математической физики: Учебное пособие для университетов. – М.: Наука, 1972.

7. Л.Э. Эльсгольц. Дифференциальные уравнения и вариационное исчисление. – М.: Наука, 1969.

8. Г.Н. Берман. Сборник задач по курсу математического анализа: Учебное пособие для вузов. – М.: Наука, 1969.

9. Д.В. Беклемишев, Л.А. Беклемишева. Сборник задач по аналитической геометрии и линейной алгебре: Учебное пособие для вузов. – М.: Наука, 1987.

10. В.Е. Гмурман. Руководство к решению задач по теории вероятностей и математической статистике: Учебное пособие для студентов вузов. – М.: Высшая школа, 1999.

11. В.А. Болгов, Б.П. Демидович и др. Сборник задач по математике для вузов. Специальные разделы математического анализа. – М.: Наука, 1981.

12. И.В. Проскуряков. Сборник задач по линейной алгебре.– М.: Наука, 1974.

13. П.Е. Данко, А.Г. Попов. Высшая математика в упражнениях и задачах. В 3-х частях. – М.: Высшая школа, 1974.

14. Д.В. Клетеник. Сборник задач по аналитической геометрии. –СПб.: Профессия, 2002.

15. И.И. Привалов. Аналитическая геометрия: Учебник для втузов. – М.: ФИЗМАТГИЗ, 1958.

16. А.Г. Курош. Курс высшей алгебры: Учебник для университетов. - М.: Наука, 1968.

Дополнительная литература

1. А.И. Мальцев. Основы линейной алгебры: Учебное пособие для студентов университетов. – М.: Наука, 1975.

2. П.Е. Данко и др. Высшая математика в упражнениях и задачах, в 2-х томах: Учебное пособие для студентов втузов. – М.: Высшая школа, 1986.

3. Г.М. Фихтенгольц. Основы математического анализа, в 2-х томах. – М.: ФИЗМАТГИЗ, 1960.

4. А.Н. Колмогоров, С.В. Фомин. Элементы теории функций и функционального анализа. – М.: Наука, 1981.

5. Х. Таха. Введение в исследование операций, в 2-х книгах. – М.: Мир, 1985.

6. Ф. А. Новиков. Дискретная математика для программистов. – СПб.: Питер, 2001.

7. В.И. Квальвассер, М.И. Фридман. Теория поля. Теория функций комплексного переменного. Операционное исчисление: Учебное пособие для втузов. – М.: Высшая школа, 1967.

8. М.А. Лаврентьев, Б.В. Шабат. Методы теории функций комплексного переменного. – М.: Наука, 1987.

9. В.С. Владимиров. Уравнения математической физики. – М.: Наука, 1971.

10. Л. А. Кальницкий и др. Специальный курс высшей математики для втузов. – М.: Высшая школа, 1976.

Наименование РГР (за полный курс математики)

1. РГР по теме: «Линейная алгебра»

2. РГР по теме: «Исследование функции и построение графика»

3. РГР по теме: «Неопределенный интеграл»

3. РГР по теме: «Определенный интеграл»

4. РГР по теме: «Дифференциальные уравнения»

5. РГР по теме: «Кратные и криволинейные интегралы»

5. РГР по теме: «Элементы теории поля»

6. РГР по теме: «Ряды»

7. РГР по теме: «Линейное программирование»

8. РГР по теме: «Теория вероятностей»

8. РГР по теме: «Математическая статистика»

Дата добавления: 2015-10-24