Вывод уравнения эллипса

Дано: эллипс с фокусами и , 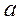– большая полуось, 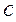– половина расстояния между фокусами. Возьмем за ось абсцисс прямую , а точку поместим на середине отрезка 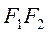. Пусть – произвольная точка плоскости. Пусть , .

По определению эллипса точка 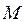принадлежит эллипсу тогда и только тогда, когда

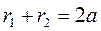. (7)

Координаты фокусов равны соответственно , , следовательно

, .

Подставим и в (7):

+ = . (8)

(8) – уравнение эллипса в заданной системе координат. Преобразуем его к виду = и возведем в квадрат обе части уравнения:

;

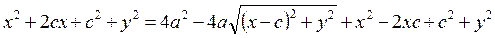
; возведем в квадрат еще раз:

;

.

Обозначим , получим .

После приведения к каноническому виду уравнение эллипса запишется так:

. (9)

Эллипс, определяемый уравнением , симметричен относительно и . - центр эллипса, и - большая и малая полуоси эллипса.

При получаем - уравнение окружности.

Определение. Эксцентриситет эллипса – отношение расстояния между фокусами к длине его большей оси: . (10)

Так как 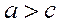, следовательно < 1.

, следовательно, .

Определение. Две прямые, перпендикулярные к большей оси эллипса и расположенные симметрично относительно центра на расстоянии от него, называется директрисами эллипса.

Их уравнения: и . Так как , следовательно, .

Гипербола

Определение. Гипербола – геометрическое место точек, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная, равная большой оси гиперболы.

Эта разность по модулю должна быть меньше расстояния между фокусами и отлична от нуля.

и - фокусные радиусы точки .

(по определению) следовательно .

Гипербола состоит из двух отдельных частей, называемых ветвями.

Канонический вид уравнения

, (11)

следовательно,

.

Уравнение – это уравнение прямой с угловым коэффициентом . При .

Прямые называются асимптотами гиперболы.

Отрезки и - оси гиперболы.

Уравнение вида задает гиперболу, сопряженную с первой.

Гипербола с равными полуосями называется равносторонней:

Определение. Эксцентриситетом гиперболы называется отношение расстояния между фокусами к расстоянию между вершинами:

. (12)

Определение. Две прямые, перпендикулярные к той оси гиперболы, которая ее пересекает, расположенные симметрично относительно центра на расстоянии от него, называются директрисами гиперболы.

Теорема. Для любой точки эллипса и гиперболы справедливо соотношение

, (13)

где 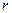– расстояние от точки до фокуса , а – расстояние до соответствующей директрисы.

Парабола

Определение. Парабола – это геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки, называемой фокусом, равно расстоянию до некоторой прямой, называемой директрисой:

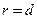. (14)

– фокус, – расстояние от фокуса до директрисы – параметр параболы, 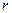– фокальный радиус точки.

(15)

– каноническое уравнение параболы, симметричной относительно оси О , при 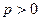ветви параболы направлены вправо. Уравнение

задает параболу, симметричную относительно оси ординат, ветви которой при 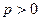направлены вверх.

Дата добавления: 2015-10-24