Геометрическое изображение комплексных чисел.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

Филиал государственного образовательного учреждения высшего

Профессионального образования «Уфимский государственный нефтяной

Технический университет» в г. Салавате

КУРС ЛЕКЦИИ ПО РАЗДЕЛАМ МАТЕМАТИКИ:

«КОМПЛЕКСНЫЕ ЧИСЛА», «ЛИНЕЙНАЯ АЛГЕБРА»,

«ВЕКТОРНАЯ АЛГЕБРА», «АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ»,

«ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ»

Составитель: Ишемгулов А.Ф., ассистент

Салават 2008

КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ.

ОПРЕДЕЛЕНИЕ КОМПЛЕКСНОГО ЧИСЛА.

Число вида , где - любые действительные числа, а - так называемая мнимая единица, называется комплексным числом.

или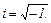

Действительные числа 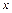и называются соответственно действительной и мнимой частями комплексного числа и обозначаются

Рассмотрим частные случаи комплексных чисел.

· Пусть 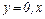- любое действительное число. Тогда становится действительным числом.

· Пусть 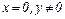. Тогда - чисто мнимое число.

Таким образом, все действительные числа и все чисто мнимые числа входят в множество комплексных чисел.

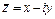Два комплексных числа и называются сопряженными комплексными числами.

Сравнение комплексных чисел осуществляется по правилам:

1. Два комплексных числа считаются равными, если .

2. Комплексное число равно нулю только тогда, когда одновременно.

3. Операции <, > не имеют смысла на множестве комплексных чисел.

ГЕОМЕТРИЧЕСКОЕ ИЗОБРАЖЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ.

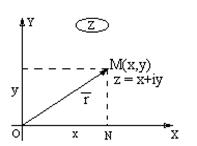Рассмотрим декартову прямоугольную систему координат ХОУ на плоскости. Каждой точке плоскости при этом соответствуют вполне определенные координаты , а следовательно, и вполне определенное комплексное число . Обратно, каждому к омплексному числу соответствует вполне определенная пара действительных чисел , а следовательно, и вполне определенная точка плоскости . Таким образом установили связь между множеством точек на плоскости и множеством комплексных чисел. Плоскость, точки которой изображают комплексные числа , называется комплексной плоскостью. Ось ОХ называется действительной осью, ось ОУ – мнимой осью. Очевидно, что изображением комплексного числа можно считать также и вектор .

Дата добавления: 2015-10-24