Геометрическая интерпретация комплексных чисел

Поставим каждому числу в соответствие точку с координатами в прямоугольной декартовой системе координат XOY, т.е. установим взаимно однозначное соответствие между множеством комплексных чисел и точками плоскости XOY (см. рис. 2.1). Плоскость XOY, служащая для изображения комплексных чисел, называется плоскостью комплексной переменной. Ось OX называется действительной осью; на ней изображаются действительные числа. Ось OY - мнимая ось; на ней изображаются чисто мнимые числа.

Сложение и вычитание комплексных чисел получают простое геометрическое истолкование. Для всякого комплексного числа вектор имеет своими проекциями на оси OX, OY соответственно числа x, y. Пусть теперь Тогда для имеем

Отсюда вытекает, что проекциями вектора 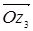на оси координат оказываются суммы соответствующих проекций векторов и ; иными словами сумма находится по правилу параллелограмма сложения векторов

.

Если то и для построения вектора 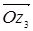в этом случае мы должны сложить векторы и - (см. рис. 2.3), т.е. получим вектор, равный вектору (вторая диагональ того же параллелограмма).

Расстояние от точки до начала координат равно Величина называется модулем комплексного числа . Для действительного числа он совпадает с понятием абсолютной величины. Модуль комплексного числа неотрицателен и определен однозначно; Угол отсчитываемый против часовой стрелки от луча до луча называется главным аргументом числа и обозначается Величина может быть найдена из системы:

Аргументом комплексного числа z (Arg z) называется любое из чисел вида где т.е. аргумент определен с точностью до Для числа z = 0 аргументом может быть любое число.

Пример. Изобразить на плоскости число 1+ i, найти его модуль и аргумент.

Решение: т.е. т.е.

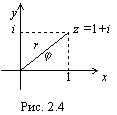
Пример. Изобразить на плоскости множество всех точек, для которых

Решение: Следовательно

или

Получили уравнение окружности радиуса 2 с центром в точке (-2; 0).

Пример. Изобразить на плоскости множество всех точек, для которых

Ответ: Луч с началом в точке (0; 0) и проходящий под углом к оси OX.

Теория комплексных чисел может быть использована при решении планиметрических задач.

Пример. Доказать, что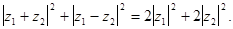

Доказательство: Поскольку то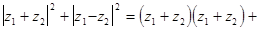

Тем самым доказано, что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

Дата добавления: 2015-10-23