Упражнения и задачи. Показать, что числа 25, -20, 16, 46, -21, 18, 37, -17 образуют полную систему вычетов по модулю

Показать, что числа 25, -20, 16, 46, -21, 18, 37, -17 образуют полную систему вычетов по модулю

Показать, что числа 24, 18, -19, 37, 38, -23, -32, 5, 41, -35, -33 образуют полную систему вычетов по модулю т = 11.

Найти наименьшие неотрицательные, наименьшие по абсолютной величине неположительные и абсолютно наименьшие вычеты чисел 24, 14, 25, 37, -8, -19, -40 по модулю 6. Какие числа из данных принадлежат к одному и тому же классу вычетов?

Доказать, что

Если два класса имеют хотя бы один общий элемент, то они совпадают. Доказать.

Наименьший неотрицательный вычет класса по модулю т равен остатку от деления а на т. Доказать.

Числа класса по модулю т образуют k классов по модулю km, а именно классы Доказать.

Приведенная система вычетов

Если т.е. а и b представляют один и тот же класс вычетов, то т.е. все числа одного класса либо имеют общий множитель с т одновременно, либо одновременно же не имеют.

Класс вычетов по модулю т, все числа которого взаимно просты с т, называется примитивным.

Приведенной системой вычетов по модулю т называется множество, состоящее из представителей примитивных классов вычетов, взятых по одному из каждого класса.

Среди чисел 0, 1, 2,..., т -1 взаимно простых с т чисел поэтому и примитивных классов

Пример. Приведенную систему вычетов по модулю 12 образуют числа 19, 23, 25, -19 или 1, 5, 7, 11, или -5, -1, 1, 5.

Приведенную систему вычетов по модулю 42 составляют числа 1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41.

Теорема. Система вычетов по модулю т является приведенной тогда и только тогда, когда в ней чисел; все числа системы взаимно просты с т и все они попарно не сравнимы по модулю т. ■

Теорема. Если и х пробегает приведенную систему вычетов по модулю т, то ах также пробегает приведенную систему вычетов по модулю т.

Доказательство: Пусть – приведенная система вычетов по модулю т. Тогда числа все взаимно просты с т и их с штук. Пусть тогда в силу того, что , получим а это неверно. Следовательно, Аналогично можно убедиться, что все пары чисел 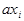и не сравнимы по модулю т для Таким образом, эти числа образуют приведенную систему вычетов. ■

Дата добавления: 2015-10-23