I. 1.1. Пример разработки модели задачи технического контроля.

ГЛАВА I.

ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.

Задачами линейного программирования называются оптимизационные задачи, в которых ограничения (представленные в виде либо уравнений, либо неравенств, либо и тех и других одновременно) и целевая функция (функция, подлежащая оптимизации) линейны. Методы ЛП широко используются для решения различных экономических, промышленных и организационных задач, в основном благодаря доступности математического обеспечения для решения задач ЛП большой размерности и возможности анализа решений при вариации исходных данных (анализа чувствительности).

I. 1. РАЗРАБОТКА МОДЕЛЕЙ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.

Термин “разработка” дословно означает построение моделей ЛП практических задач. Это скорее искусство, которое постигается с опытом.

Отметим основные этапы этой задачи:

· определение переменных задачи;

· представление ее ограничений в виде линейных уравнений или неравенств;

· задание линейной целевой функции, подлежащей минимизации или максимизации.

I. 1.1. Пример разработки модели задачи технического контроля.

Предположим, что в отделе технического контроля (ОТК) некоторой фирмы работают контролеры двух категорий. Норма выработки ОТК за 8-ми часовую смену - не менее 1800 изделий. Контролер I категории проверяет 25 изделий в час, и не допускает ошибок в 98% случаев. Контролер II категории, соответственно, проверяет 15 изделий в час, его точность составляет 95%.

Зарплата контролера I категории - 4$ в час, контролер II категории получает 3$ в час. Вместе с тем, при каждой ошибке контролера фирма несет убытки в размере 2$.

Фирма может использовать не более 8 контролеров I категории и 10 контролеров II категории.

ЗАДАЧА: подобрать оптимальный состав ОТК, при работе которого, фирма бы несла минимальные затраты.

Разработка модели: Пусть и 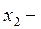количество контролеров I и II категории в отделе. Их число ограничено

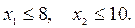
В смену необходимо проверять не менее 1800 изделий. Следовательно необходимо выполнение неравенства

или, после упрощения

В расходах фирмы отмечаются два момента: зарплата контролера и его ошибки.

Расходы фирмы на контролера I категории: 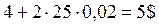в час, на контролера II категории: в час.

Таким образом, функция

при ограничениях

Дата добавления: 2015-10-29