
|
Читайте также: |
Каждой задаче линейного программирования

со смешанными ограничениями вида

можно поставить в соответствие другую задачу, которая называется двойственной по отношению к первой. Она выглядит следующим образом

при ограничениях

Обе приведенные выше задачи образуют так называемую двойственную пару. Совместное рассмотрение таких пар задач позволяет исследовать влияние изменения управляемых и неуправляемых переменных системы на значение целевой функции, проводить экономический анализ результатов расчетов. Сопоставляя записи прямой и двойственной задач, можно установить следующие взаимосвязи:
· если прямая задача является задачей максимизации, то двойственная - минимизации и наоборот;
· коэффициенты целевой функции прямой задачи становятся свободными членами ограничений двойственной задачи;
· свободные члены ограничений прямой задачи становятся коэффициентами целевой функции двойственной задачи;
· матрица ограничений двойственной задачи получается транспонированием матрицы ограничений прямой задачи;
· число переменных двойственной задачи равно числу ограничений прямой задачи и наоборот.
Взаимно однозначное соответствие между переменными исходной задачи и ограничениями двойственной задачи удовлетворяет следующему положению: 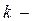 е ограничение двойственной задачи будет неравенством, если на е ограничение двойственной задачи будет неравенством, если на 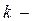 ю переменную исходной задачи наложено требование неотрицательности, если же ю переменную исходной задачи наложено требование неотрицательности, если же 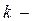 я переменная не ограничена в знаке, то я переменная не ограничена в знаке, то 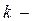 е ограничение будет уравнением. е ограничение будет уравнением.
|
Основное содержание связи между задачами двойственной пары заключается в том, что решая симплекс-методом одну из них, автоматически получается решение другой. Для этого достаточно воспользоваться соответствием переменных прямой и двойственной задач и оценок в последней симплекс-таблице:
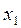
| 
| ... | 
| ... | 
| 
| 
| ... | 
| ... | 
|

| 
| ... | 
| ... | 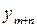
| 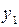
| 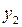
| ... | 
| ... | 
|

| 
| ... | 
| ... | 
| 
| 
| ... | 
| ... | 
|
Отсюда имеем оптимальный план двойственной задачи.
· Если прямая задача решается на максимум:

· Если прямая задача решается на минимум:

Рассмотрим пример.

Приведем задачу к каноническому виду

Таблица I.
| № 1 | |||||||

| 
| 
| 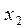
| 
| 
| 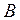
| 
|

| 
| ||||||

| 
| ||||||

| 
|
Здесь в условиях наших обозначений:  (количество истинных переменных) и
(количество истинных переменных) и  (количество дополнительных переменных = количеству ограничений задачи):
(количество дополнительных переменных = количеству ограничений задачи):

| 
| 
| 
|

| 
| 
| 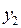
|

| 
| 
| 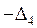
|
Заметим так же, что задача решается на максимум.
Таблица II.
| № 2 | |||||||

| 
| 
| 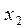
| 
| 
| 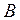
| 
|

| 
| 
| 
| ||||

| 
| 
| 
| ||||

| -2 | 
|
Таблица III.
| № 3 | |||||||

| 
| 
| 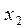
| 
| 
| 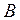
| 
|

| 
| 
| 
| - | |||

| 
| 
| 
| - | |||

| 
| 
| 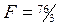
|

Оптимальный план двойственной задачи, судя по вектору  , будет иметь вид
, будет иметь вид 
Дата добавления: 2015-10-29; просмотров: 212 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ | | | I. 3.2. Двойственный симплекс-метод. |