I. 3.2. Двойственный симплекс-метод.

Перейдем теперь к построению задачи двойственной к рассмотренной выше. В соответствии с правилами построения, она примет вид

система ограничений:

Базис пространства переменных прямой задачи, в котором выполнены все ограничения двойственной задачи, будем называть сопряженным базисом.

Введем следующие обозначения:

и в качестве сопряженного базиса возьмем, например, векторы Тогда из системы (см. систему ограничений двойственной задачи):

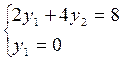
найдем значение опорного плана двойственной задачи:

Становится очевидным, что данный базис не может быть взят в качестве сопряженного, так как при и 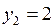второе ограничение системы не выполняется. Тогда, попробуем в качестве сопряженного базиса выбрать векторы Из системы:

находим значения Неравенство

при этих значениях выполняется и, следовательно, система векторов в самом деле может рассматриваться в качестве сопряженного базиса двойственной задачи.

Далее, определим коэффициенты разложения небазисных векторов по векторам базиса и найдем псевдоплан исходной задачи:

Очевидно, что базисные векторы будут иметь вид

Так как среди компонент разложения вектора по сопряженному базису имеются отрицательные, то критерий оптимальности не выполнен, то есть указанный план не доставляет минимального значения функции и за счет перехода к новому базису ее значения можно еще уменьшить.

Заполняем первую таблицу (см. таблица I) и приступаем к итерациям.

Таблица I.

№ 1
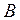
		-18			-5	-39
		-

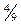
Результат итераций будем записывать в таблицу II.

Таблица II.

№ 2
	-	-	-	-

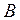
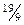
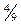
В столбце свободных членов (он выделен в таблице II) нет отрицательных элементов, следовательно, полученный план: - оптимален.

Количество операций, необходимое для одной итерации в симплекс-методе и двойственном симплекс-методе, соизмеримо. Однако, двойственный симплекс-метод целесообразно использовать при решении таких задач ЛП, в которых нахождение начального допустимого базисного решения затруднительно (например, приходится вводить искусственные переменные), а начальный псевдоплан определяется автоматически.

[1] Множество точек называется выпуклым, если оно вместе с любыми двумя точками содержит и их произвольную выпуклую линейную комбинацию (линейную оболочку).

[2] Две граничные точки некоторого отрезка, состоящего из граничных точек ОДР, называются крайними. Точка называется граничной для некоторого множества точек 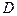, если для любого сколь угодно малого в окрестности ее находятся и точки множества, и точки ему не принадлежащие.

[3] Будем обозначать их 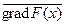или кратко .

[4] Соседняя вершина ОДР - смежное допустимое решение.

Дата добавления: 2015-10-29