Знак отрицания можно ввести под знак квантора, заменив на двойственный.

Рассмотрим выражение: (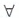 хФ(х)).

Это есть высказывание: «Отрицается то, что для любого элемента х предикат Ф(х) будет иметь значение И.» Оно равносильно высказыванию «существует элемент х, для которого Ф(х) имеет значение Л.», или, что то же, «существует элемент х, для которого (Ф)(х) имеет значение И». Следовательно, исходное выражение равносильно последнему высказыванию, т.е.

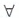( хФ(х))= х(Ф)(х).

Рассмотрим другое выражение: ( хФ(х)).

Это есть высказывание «отрицается то, что существует эл-т х, для которого Ф(х) имеет значение И.» Значит оно равносильно высказыванию: «для всех х предикат Ф(х) имеет значение Л.» Это высказывание равносильно следующему: «для всех х предикат (Ф)(х) имеет значение И». Следовательно, исходное высказывание равносильно последнему высказыванию, т.е.

( хФ(х))= 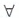х(Ф)(х).

Эти равносильности являются законами де Моргана для кванторов.

Доказать примитивную рекурсивность

17) f(x,y)=(x+y)

Док-во:

_/ ¯f(x,0)=g(x)=x

\_f(x,y+1)=h(x,y, f(x,y))= f(x,y)+1

По схеме примитивной рекурсии имеем:

f(x, 0) = g(x)=x,

f(x, 1) = h(x, 0, f(x, 0)) = x + 1,

f(x, 2) = h(x, 1, f(x, 1)) = x + 2,

f(x, 3) = h(x, 2, f(x, 2)) = x + 3,

…………………………………

f(x, i) = h(x, (i-1), f(x, (i -1))) = x + i.

Если i = у, то f(x, у) = (x+у). Пусть x=3, у=6, тогда f+(3, 6) = 3+6 = 9.

Так, используя базовые функции тождества(g) и следования(h), можно вычислять значения функции сложения f(x, у) = (x+y) = R(x, (f(x, у)+1)). (где R – оператор рекурсии).

18) f(x,y)=(x ÷ y)

Док-во:

f(x,y)=(x ÷ y)=

_/ ¯x-y, если x>y

\_0, если x <или= y

_/ ¯f(x,0)=g(x)=x

\_ f(x,y+1)=h(x,y, f(x,y))= f(x,y) ÷1

По схеме примитивной рекурсии имеем:

f (x, 0) = g(x) = x,

f (x, 1) = h(x, 0, f (x, 0)) = x÷1,

f (x, 2) = h(x, 1, f (x, 1)) = (x÷1)÷1=x÷2,

...............................................................

f (x, i) = h(x, i, f(x, i)) = (x÷(i-1))÷1=x÷i.

Если i=y, то f (x, y) = x÷y. Пусть х = 6, y = 3, тогда f (6, 3) = 6÷3 = 3.

Так, используя базовую функцию тождества(g) и примитивно рекурсивную

функцию предшествования(h), можно вычислять значение функции усеченного вычитания f (x, y)=R(x, f(x,y) ÷1))=(x÷y).

19) f(x,y)=(x* y)

Док-во:

_/ ¯f(x,0)=g(x)=0

\_ f(x,y+1)=h(x,y, f(x,y))=x+f(x,y)

По схеме примитивной рекурсии имеем:

f (x,0) = g(x) = 0,

f (x,1)= h(x, 0, f (x, 0)) = x+0 = x,

f (x, 2)= h(x, 1, f (x,1)) = (x+x) = 2*x,

f (x, 3)= h(x, 2, f (x, 2)) = (x+2*x) = 3*x,

…………………………………………….

f (x,i) = h(x, (i - 1),f (x, i-1)) = (x+(i - 1)*x) = i*x.

Если i = у, то f (x, y) = x*у. Пусть х=3, y=4. Тогда f (3, 4)=3*4 =12

Так, используя базовую функцию константы(g(x)=0) и примитивно рекурсивную функцию сложения(h), можно вычислять значения функции умножения: f(x,y) = R(0, f(x,f(x, y)))=(x*у)

20) f(x,y)=(x^ y)

Док-во:

_/ ¯f(x,0)=g(x)=1

\_ f(x,y+1)=h(x,y, f(x,y))=x*f(x,y)

По схеме примитивной рекурсии имеем:

f(x,0)=g(x)=1;

f(x,1)=h(x, 0, f(x, 0))=x*1= x;

f(x,2)=h(x, 1, f(x, l))=x*x=x^2;

f(x, 3)=h(x, 2, f(x, 2))=x*x^2=x^3,

………………………………………………..

f(x, i)=h(x, (i - 1), f(x, (i - 1)))=x*x^(i - 1) = x^i

Если i=у, то f(x, y)=x^y. Пусть x=3, у=3, тогда f(3, 3)=3^3=27.

Так, используя базовую функцию(g(x)=1) и рекурсивную функцию умножения(h), можно вычислять значения рекурсивной функции возведения в степень x^y =R(1, f(x, f(x, y)))=f(x, y).

Дата добавления: 2015-10-30