I. 4.1. Первая теорема двойственности.

I. 4. ОСНОВНЫЕ УТВЕРЖДНЕИЯ ТЕОРИИ ДВОЙСТВЕННОСТИ

И ИХ ЭКОНОМИЧЕСКОЕ СОДЕРЖАНИЕ.

I. 4.1. Первая теорема двойственности.

Здесь, в первую очередь, по структуре прямой и двойственной задач (в их канонической постановке), важно отметить, что для любых допустимых планов 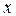и (каждой из пары взаимодвойственных задач) справедливо неравенство

С экономической точки зрения, это означает, что для любого допустимого плана производства 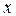и любого допустимого вектора оценок ресурсов общая созданная стоимость не превосходит суммарной оценки ресурсов.

Очевидно, что можно найти такие допустимые и пары двойственных по отношению друг к другу задач, для которых выполняется соотношение В этом случае и - оптимальные планы соответствующих задач. Это утверждение - достаточный признак оптимальности, носит название критерияоптимальности Канторовича. Его экономический смысл следующий: план производства 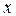и вектор оценок ресурсов являются оптимальными, если цена всей произведенной продукции и суммарная оценка ресурсов совпадают.

Заметим, что для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование дополнительного плана для каждой из них.

Теорема (первая теорема двойственности): если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем соответствующие экстремальные значения целевых функций совпадают: Если одна из двойственных задач неразрешима в следствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.

Таким образом, если задача определения оптимального плана, максимизирующей выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукта, совпадает с суммарной оценкой ресурсов. Совпадения значений целевых функций для соответствующих решений пары двойственных задач достаточно для того, чтобы эти решения были оптимальными. Это значит, что план производства и вектор оценок ресурсов являются оптимальными тогда и только тогда, когда цена произведенной продукции и суммарная оценка ресурсов совпадают. Оценки выступают как инструмент балансирования затрат и результатов. Двойственные оценки обладают тем свойством, что они гарантируют рентабельность оптимального плана, то есть равенства общей оценки продукции и ресурсов; обуславливает убыточность всякого другого плана, отличного от оптимального. Двойственные оценки позволяют сопоставлять и балансировать затратыи результаты системы.

Напомним, что как уже было отмечено ранее, связь между задачами двойственной пары глубже, нежели указано в формулировке теоремы: решая симплекс-методом одну из них, автоматически получается решение второй задачи.

I. 4.2. Вторая теорема двойственности и ее экономическое содержание.

Здесь мы сразу приведем формулировку этой теоремы.

Теорема (о дополняющей нежесткости): для того, чтобы планы и пары двойственных задач были оптимальными, необходимо и достаточно выполнение условий:

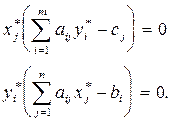
Это условия дополняющей нежесткости. Из них следует: если какое-либо неравенство системы ограничений одной из задач не обращается в тождество оптимальным планом этой задачи, то соответствующая компонента оптимального плана двойственной задачи должна равняться нулю; если же какая-либо компонента оптимального плана одной из задач положительна, то соответствующее ограничение в двойственной задаче ее оптимальным планом должно обращаться в тождество, то есть, если:

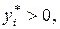то если то

Точно так же, если:

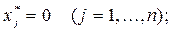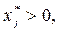то если то

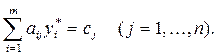
Экономически это можно интерпретировать следующим образом. Если по некоторому оптимальному плану производства, расход го ресурса строго меньше его запасов , то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса равна нулю. Если в некотором оптимальном плане оценок его я компонента строго больше нуля, то в оптимальном плане производства расход соответствующего ресурса равен его запасу.

Отсюда следует вывод: двойственные оценки могут служить мерой дефицитности ресурсов. Дефицитный ресурс (полностью используемый по оптимальному плану производства) имеет положительную оценку, а избыточный ресурс (используемый не полностью) имеет нулевую оценку.

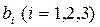ПРИМЕР: Продукция в цехе может производиться тремя технологическими способами Объемы ресурсов и их расход в единицу времени для каждой технологии, а также производительности (эффективности) технологий (в денежных единицах за единицу времени работы по данной технологии) представлены в таблице данных.

Определим оптимальный план использования каждого технологического способа , то есть время использования каждого технологического способа (запишем решение двойственной задачи и проверим условия о дополняющей нежесткости).

Таблица данных

Ресурсы	Технологические способы	Объем ресурса
Рабочая сила (чел.-ч.)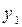
Сырье (т)			2,5
Электроэнергия (кВт.ч)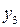
Производительность технологического способа
План

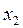
ПРЯМАЯ ЗАДАЧА

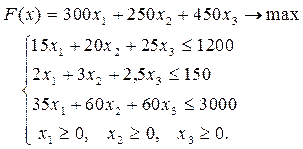
ДВОЙСТВЕННАЯ ЗАДАЧА

РЕШЕНИЕ ПРЯМОЙ ЗАДАЧИ СИМПЛЕКС-МЕТОДОМ

№ 1
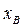
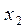
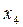
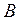
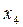
				2,5

№ 2
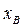
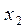
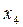
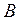
		0,6	0,8		0,04
		0,5			-0,1
		-1			-2,4				-
		-110		-18

№ 3
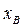
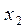
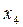
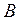
			-0,4		0,16	-1,2
					-0,2
					-2,6
		-170		-12	-60

Оптимальный план использования технологий:

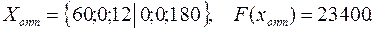
Таким образом, первую технологию целесообразно использовать в течение 60 часов, третью - 12 часов, а вторую технологию применять вовсе даже нецелесообразно. При этом продукции будет выпущено на 23400 ден. единиц.

Решение двойственной задачи: Так как то первый и второй ресурсы использованы полностью. Третий ресурс избыточен Его двойственная оценка равна нулю: 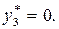Следовательно, если при м технологическом способе суммарная оценка ресурсов, идущих на производство единицы продукции, выше дохода 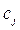, то данный способ не должен внедряться 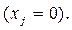Если же й технологический способ используется в оптимальном плане, то суммарная оценка ресурсов, необходимых для производства единицы продукции, равна доходу .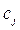

Теперь проверим условия о дополняющей нежесткости.

ДЛЯ ПРЯМОЙ ЗАДАЧИ

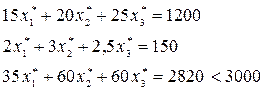
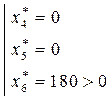
ДЛЯ ДВОЙСТВЕННОЙ ЗАДАЧИ

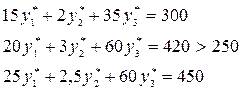
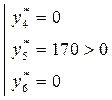
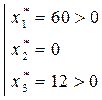
Условия дополняющей нежесткости выполняются.

I. 4.3. Третья теорема двойственности и ее экономическое содержание.

Сразу приведемееформулировку.

Теорема (третья теорема двойственности): двойственные оценки показывают приращение целевой функции, вызванные малыми изменениями свободного члена соответствующего ограничения задачи линейного программирования, то есть

Выясним экономическое содержание третьей теоремы двойственности. Для этого в выражении, указанном в формулировке теоремы, дифференциалы заменим приращениями, то есть Получим при имеем

Двойственная оценка численно равна изменению целевой функции при изменении соответствующего ресурса на единицу. Их часто называют скрытыми, теневыми или маргинальными оценками ресурсов.

В качестве иллюстрации этого, в предыдущей задаче о выборе оптимальной технологии, выясним экономический смысл двойственных переменных.

Из последней таблицы получено решение двойственной задачи:

Как следует из решения, первый и второй ресурсы потребляются полностью. Их двойственные оценки положительны. Приращение первого ограниченного ресурса на единицу ведет к увеличению целевой функции на 12, второго - на 60,третий ресурсизбыточен: Его двойственная оценка равна нулю: 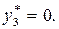Поэтому дальнейшее его увеличение не окажет влияния на значение целевой функции.

Возникает вопрос: что же показывают значения дополнительных двойственных оценок Оптимальный план исходной задачи:

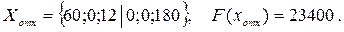
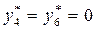говорит о том, что первую технологию целесообразно использовать в течение 60 часов, третью - 12часов. Вторая технология вообще не должна внедряться. Она заведомо убыточная. Если ее все же использовать, то она в течение каждого часа работы будет снижать достигнутый уровень выпуска на ден. единиц. Значения . Это свидетельствует о том, что первая и третья технологии не являются убыточными. В самом деле, из второго ограничения двойственной задачи следует:

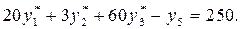
Стоимость ресурсов, используемых в единицу времени при работе по второму технологическому способу, составит:

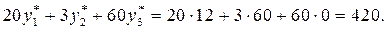
В единицу же времени этот способ может дать продукции на 250 ден. единиц. Поэтому убыток в единицу времени при работе этим способом составит

Дата добавления: 2015-10-29