I.5.7. Mодификация (изменение) данных задачи.

Для входа в режим модификации необходимо выбрать пункт 7 в меню задачи линейного программирования (“Modify problem”). После этого на экране появится меню выбора модифицируемых элементов задачи (см. Фиг. 18).

Option Menu for Modifying yyy Меню режимов для модификации <имя задачи>
Option Режим
	Modify the objective function coefficients Изменить коэффициенты целевой функции
	Modify one constraint Изменить одно ограничение
	Add one constraint Добавить одно ограничение
	Delete one constraint Удалить одно ограничение
	Add one variable Добавить одну переменную
	Delete one variable Удалить одну переменную
	Display/ print input data Просмотр/печать исходных данных
	Return to the functional menu Возврат в функциональное меню

Передвигая курсор вверх или вниз выберите режим и нажмите ENTER.

Фиг. 18. Меню выбора режимов модификации задачи.

После входа в режим модификации (любое изменение) программа запрашивает новое имя задачи, как показано на Фиг. 19.

Current problem (model) name: yyy Существующее имя задачи (модели): <имя задачи> What is the new problem (model) name? Какое новое имя задачи (модели)?

Фиг. 19. Запрос имени модифицированной задачи.

При модификации ограничений, программа запрашивает номер ограничения, как показано на Фиг. 20.

Modify a Current Модификация ограничения Type the constraint number, enter 0 to return to the menu. Введите номер ограничения или 0 для возврата в меню модификации.   Which constraints? Какое ограничение?

Фиг. 20. Запрос номера модифицируемого ограничения.

При добавлении ограничения на экран выдается маска для ввода этого ограничения, показанная на Фиг. 21.

Add One Constraint Page 2 Добавить одно ограничение Страница 2   (3) ___________X1___________X2 _________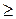

Фиг. 21. Маска для ввода дополнительного ограничения.

При удалении ограничения программа запрашивает номер ограничения, как показано на Фиг. 22.

Delete One Constraint Удалить одно ограничение Type the constraint number, enter 0 to return to the menu. Введите номер ограничения или 0 для возврата в меню модификации.   Which constraints? Какое ограничение?

Фиг. 22. Запрос номера удаляемого ограничения.

Пакет программ QSB предусматривает возможность добавления либо удаления переменных задачи. Протокол диалога программы с пользователем при добавлении одной переменной показан на Фиг.23.

Are you sure to add one variable (Y/N)? Вы уверены, что хотите добавить одну переменную (Y/N)? What is the variable name (default is Xn)? Какое имя переменной (стандартное - Xn)?   Add One Variable Добавить одну переменную   Coefficient of X3 in objective function? Коэффициент при X3 в функции цели? Coefficient of X3 in constraint 1? Коэффициент при X3 в ограничении 1? и так далее...

Фиг. 23. Протокол диалога при добавлении переменной.

ВАРИАНТЫ ИСХОДНЫХ ДАННЫХ

В режиме использования вычислительной техники (пакет ППП QSB) предлагается решить следующую задачу производственного планирования.

Изготовление продукции двух видов (П1 и П2) требует использования четырех видов сырья - 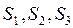и 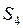. Запасы сырья ограничены и составляют соответственно 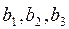и 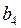условных единиц. Количество единиц сырья, используемое для изготовления единицы продукции каждого вида определяется технологией производства и показано в таблице 1. Прибыль, получаемая предприятием при реализации единицы продукции каждого вида составляет соответственно 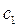и 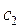условных единиц.

Необходимо разработать план выпуска продукции, учитывающий имеющиеся запасы сырья и обеспечивающий предприятию максимальную прибыль при реализации выпущенной продукции.

Таблица 1 (исходных данных)

		Количество единиц сырья, необходимое для производства единицы продукции вида:
Вид сырья	Имеющийся запас сырья (усл.единиц)	П1	П2
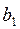
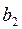
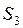
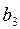
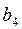
Прибыль от реализации единицы продукции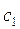

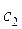
Варианты индивидуальных заданий (таблица 2).

Таблица 2 (исходных данных)

Номер	Запасы сырья каждого вида	Прибыль от реализации единицы продукции
варианта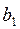

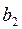
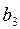
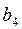
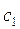
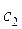
Дата добавления: 2015-10-29