
Читайте также:
|
I. Предположим, что в производстве двух видов продукции  и
и  принимают участие три предприятия. При этом на изготовление единицы изделия
принимают участие три предприятия. При этом на изготовление единицы изделия  первое предприятие тратит
первое предприятие тратит  часов, второе предприятие -
часов, второе предприятие - 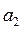 часов, третье предприятие -
часов, третье предприятие -  часов. На изготовление единицы продукции вида
часов. На изготовление единицы продукции вида  первое предприятие тратит
первое предприятие тратит 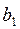 часов, второе предприятие -
часов, второе предприятие -  часов, третье предприятие -
часов, третье предприятие -  часов. На производство всех видов продукции первое предприятие может затратить не более, чем
часов. На производство всех видов продукции первое предприятие может затратить не более, чем 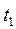 часов, второе предприятие - не более, чем
часов, второе предприятие - не более, чем  часов, третье предприятие - не более, чем
часов, третье предприятие - не более, чем  часов. От реализации единицы готовой продукции вида
часов. От реализации единицы готовой продукции вида  прибыль составляет
прибыль составляет  , а вида
, а вида  -
- 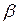 денежных единиц.
денежных единиц.
Составить математическую модель, определения максимальной прибыли от реализации всей продукции видов  и
и  . Решить задачу симплекс-методом. Дать геометрическую интерпретацию математической формулировки. Данные приведены в таблице данных I.
. Решить задачу симплекс-методом. Дать геометрическую интерпретацию математической формулировки. Данные приведены в таблице данных I.
Таблица данных I.
| № Варианта |

|
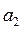
|

|
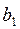
|

|

|
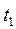
|

|

|

|
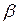
|
| I | |||||||||||
| II | |||||||||||
| III | |||||||||||
| IV | |||||||||||
| V | |||||||||||
| VI | |||||||||||
| VII | |||||||||||
| VIII | |||||||||||
| IX | |||||||||||
| X |
II. Предположим, что для производства двух видов продукции  и
и  можно использовать только материал трех сортов. При этом на изготовление единицы изделия вида
можно использовать только материал трех сортов. При этом на изготовление единицы изделия вида  расходуется
расходуется  кг материала 1-го сорта,
кг материала 1-го сорта, 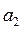 кг материала 2-го сорта и
кг материала 2-го сорта и  кг материала 3-го сорта. На изготовление единицы изделия вида
кг материала 3-го сорта. На изготовление единицы изделия вида  расходуется
расходуется 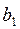 кг материала 1-го сорта,
кг материала 1-го сорта,  кг материала 2-го сорта и
кг материала 2-го сорта и  кг материала 3-го сорта. На складе фабрики имеется всего материала первого сорта
кг материала 3-го сорта. На складе фабрики имеется всего материала первого сорта  кг, материала второго сорта
кг, материала второго сорта  и материала третьего сорта
и материала третьего сорта 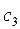 кг. От реализации единицы готовой продукции вида
кг. От реализации единицы готовой продукции вида  фабрика имеет прибыль
фабрика имеет прибыль  , а от реализации продукции вида
, а от реализации продукции вида  прибыль составляет
прибыль составляет 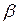 денежных единиц.
денежных единиц.
Составить математическую модель, определения максимальной прибыли от реализации всей продукции видов  и
и  . Решить задачу симплекс-методом. Дать геометрическую интерпретацию математической формулировки. Данные приведены в таблице данных II.
. Решить задачу симплекс-методом. Дать геометрическую интерпретацию математической формулировки. Данные приведены в таблице данных II.
Таблица данных II.
| № Варианта |

|
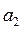
|

|
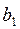
|

|

|

|

|
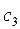
|

|
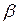
|
| I | |||||||||||
| II | |||||||||||
| III | |||||||||||
| IV | |||||||||||
| V | |||||||||||
| VI | |||||||||||
| VII | |||||||||||
| VIII | |||||||||||
| IX | |||||||||||
| X |
Дата добавления: 2015-10-29; просмотров: 152 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| I. 2.3. Табличный симплекс-метод. | | | I. 3.1. Двойственная задача линейного программирования. |