
|
Читайте также: |
ГЛАВА II.
СПЕЦИАЛЬНЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.
II. 1. ТРАНСПОРТНЫЕ ЗАДАЧИ.
II. 1.1. Общая постановка задачи.
Транспортные задачи составляют особый класс задач линейного программирования, специфика математических моделей которых позволяет применять для их решения наряду с общими методами решения задач ЛП специальные методы, значительно сокращающие процесс вычислений. Простейшая постановка транспортной задачи (Т-задачи) по критерию стоимости следующая.
В 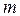 пунктах производства
пунктах производства 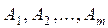 имеются запасы какого-то продукта в количествах
имеются запасы какого-то продукта в количествах 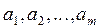 единиц соответственно. Необходимость в этом продукте в пунктах потребления
единиц соответственно. Необходимость в этом продукте в пунктах потребления 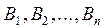 выражается соответственно величинами
выражается соответственно величинами 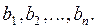 Из каждого пункта производства возможна транспортировка продукта в любой пункт потребления. Транспортные издержки на перевозку единицы продукции (груза) из пункта
Из каждого пункта производства возможна транспортировка продукта в любой пункт потребления. Транспортные издержки на перевозку единицы продукции (груза) из пункта 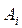 и
и 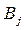 заданы и составляют
заданы и составляют 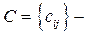 так называемую матрицу издержек.
так называемую матрицу издержек.
| Задача состоит в том, чтобы отыскать такой план перевозок, при котором весь продукт из пунктов производства будет вывезен, запросы потребителей полностью удовлетворены и суммарные транспортные издержки - минимальны. |
Условие Т-задачи представим в виде:
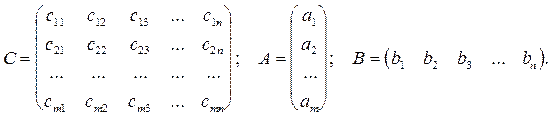
Здесь 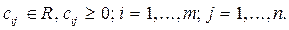 Для составления математической модели задачи, введем переменные
Для составления математической модели задачи, введем переменные 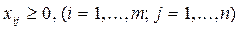 , обозначающие количество груза, перевозимого из
, обозначающие количество груза, перевозимого из  го пункта производства в
го пункта производства в 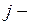 й пункт потребления.
й пункт потребления.
Требуется найти множество переменных 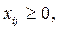 минимизирующих функцию
минимизирующих функцию
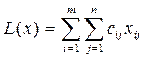
и удовлетворяющих условиям
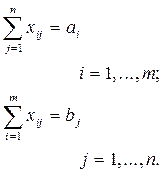
Т-задача представляет собой задачу ЛП с числом переменных 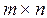 и числом ограничений типа равенств
и числом ограничений типа равенств 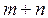 .
.
Набор переменных 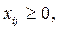 удовлетворяющий условиям Т-задачи, можно записать в виде матрицы
удовлетворяющий условиям Т-задачи, можно записать в виде матрицы
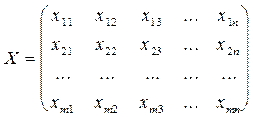
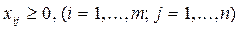 .
.
Матрицу 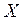 называют планом перевозки Т-задачи, а переменные
называют планом перевозки Т-задачи, а переменные  называют собственно перевозками.
называют собственно перевозками.
План, при котором значение целевой функции минимально (и его уже сделать меньшим нельзя в области ограничений Т-задачи) называется оптимальным. Матрица 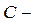 матрица издержек.
матрица издержек.
В ограничениях Т-задачи первое условие гарантирует полный вывоз продукта из всех пунктов производства, второе условие означает полное удовлетворение спроса на этот продукт в пунктах потребления.
На практике же встречаются как задачи, где выполняется равенство между суммарными ресурсами и суммарными потребностями (условие баланса)
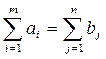
так и задачи, где эти условия не выполнены. В исходной постановке, где выполнено условие баланса, задача называется закрытой моделью. В противном случае - модель открыта и тогда ее необходимо “ закрыть ”. Если
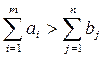 ,
,
вводится дополнительный пункт потребления, в котором потребности

если же
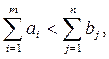
то вводится дополнительный пункт производства. В таблице издержек стоимости перевозок по соответствующим маршрутам равны нулю, так как введенные пункты фактически являются фиктивными и в перевозках они не участвуют.
Существуют различные подходы в решении Т-задачи. В частности к ручным методам вычисления оптимального плана относятся распределительный метод и методпотенциалов. Т-задачи можно решать и с использованием вычислительной техники с помощью методов дифференциальных рент и так называемого Венгерского метода.
| Решение Т-задачи “ручными” методами состоит из следующих основных этапов: · определение исходного опорного плана задачи; · оценка этого плана; · переход к следующему, лучшему плану путем замены одной из базисных переменных на свободную. |
II. 1.2. Метод определения начального опорного плана перевозок.
Как и в других задачах ЛП, итерационный процесс отыскания оптимального плана транспортной задачи начинается с какого-либо опорного плана. Опорный план Т-задачи строим в виде матрицы размеров 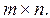 Заполненные позиции матрицы, то есть, в которых
Заполненные позиции матрицы, то есть, в которых 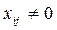 , соответствуют базисным переменным. Для невырожденного опорного плана их количество равно
, соответствуют базисным переменным. Для невырожденного опорного плана их количество равно 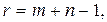 где
где 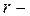 ранг[1] матрицы системы ограничений.
ранг[1] матрицы системы ограничений.
Начальный опорный план может быть построен, например, методом северо-западного угла [2].
Определим элементы матрицы  начиная с верхнего левого угла. Находим величину
начиная с верхнего левого угла. Находим величину 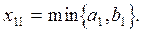 Если
Если 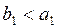 , то
, то  , и первый столбец закрыт для расчета остальных элементов, то есть
, и первый столбец закрыт для расчета остальных элементов, то есть 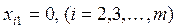 . Если
. Если 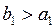 , то
, то 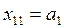 , и первый столбец закрыт для расчета остальных элементов, то есть
, и первый столбец закрыт для расчета остальных элементов, то есть  .
.
Затем вычисляем
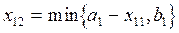 при
при 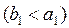 ,
,
либо
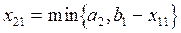 при
при 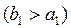 .
.
Этот процесс продолжается до тех пор, пока на каком-то этапе не исчерпаются ресурсы  и не удовлетворятся потребности
и не удовлетворятся потребности  .
.
Существуют и другие методы определения начального плана перевозок.
Дата добавления: 2015-10-29; просмотров: 219 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ПРОГРАММИРОВАНИЯ. | | | Метод двойного предпочтения. |