Наибольший общий делитель. Алгоритм Евклида

Если d делит а и d делит b, то d - общий делитель чисел а и b. Так как делителей чисел а и b конечное число, то и общих делителей чисел а и b конечное число. Среди любого конечного числа целых чисел существует наибольшее. Наибольший из общих делителей называется наибольшим общим делителем чисел а и b и обозначается НОД или просто Аналогично вводится наибольший делитель нескольких целых чисел Если наибольший общий делитель чисел равен 1, то эти числа называются взаимно простыми. Числа попарно взаимно простые являются и взаимно простыми, но числа взаимно простые не обязательно попарно взаимно простые. Например, числа 10, 12, 27 взаимно простые, но пары 10 и 12, 12 и 27 имеют общие множители.

Алгоритм Евклида нахождения наибольшего общего делителя двух целых чисел. Пусть а и b – положительные целые числа и Применим теорему о делении с остатком несколько раз:

............

Процесс деления предыдущего остатка на следующий конечен, так как в последовательности:

может быть только конечное число чисел (не более, чем b чисел).

Пусть х – общий делитель чисел а и b. Тогда двигаясь от равенства к следующему, начиная с первого, получим делится на х, делится на х и т.д., делится на х. Двигаясь же от последнего равенства к первому, заметим, что делится на делится на и т.д., b делится на , а делится на . Таким образом, - общий делитель чисел а и b, делящийся на любой другой общий делитель этих чисел, т.е. Таким образом, последний ненулевой остаток в алгоритме Евклида – наибольший общий делитель.

Пример. Найти НОД(1173, 323).

Решение:

Ответ: 17.

Упражнения и задачи

Найти наибольший общий делитель систем чисел:

а) 546 и 231; б) 1001 и 6253; в) 1517 и 2257;

г) 2737, 9163 и 9639; д) 1411, 4641 и 5253.

Доказать, что если то

Доказать, что если а делится на b, то

Для любого целого положительного числа т доказать равенство:

Если то Доказать.

Доказать, что

Доказать, что для любых натуральных а и b имеет место равенство:

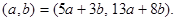
Если то Доказать.

Дата добавления: 2015-10-23