Основная теорема арифметики кольца целых чисел

Теорема. Любое натуральное число, отличное от 1, можно представить в виде произведения простых чисел и притом единственным образом с точностью до порядка следования сомножителей.

Доказательство теоремы существования проведем методом полной математической индукции по числу п.

База индукции. Простое число мы рассматриваем как произведение простых чисел, состоящее из одного множителя. Поэтому для простых чисел утверждение теоремы существования верно и, в частности, для числа 2.

Гипотеза индукции. Предположим, что утверждение теоремы верно при всех k, для которых

Право перехода. Обозначим через p наименьший целый положительный отличный от 1 делитель числа п. Ясно, что p – простое число и Если то утверждение теоремы верно. Если то к можно применить предположение индукции, так как Тогда , а следовательно и п можно представить в виде произведения простых чисел. Теорема существования доказана.

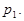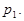Доказательство теоремы единственности проведем методом от противного. Пусть для некоторого натурального числа п имеется два представления в виде произведения простых чисел и пусть Предположим, что Тогда и произведение делится на По теореме Евклида отсюда следует, что делится на Повторяя рассуждения при предположении получим, что 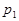должно равняться одному из чисел Изменив нумерацию, можно добиться того, что Итак, мы имеем равенство:

где

Отсюда

Вновь повторяя рассуждения, получим 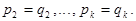Равенство невозможно, т.е. Предположение приводит к такому же противоречию. Остается лишь одна возможность Итак, представления оказались тождественны. Теорема доказана. ■

В разложении числа п на простые сомножители некоторые простые числа могут повторяться. Собирая одинаковые сомножители в степени, получим каноническое представление числа п:

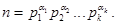
Из основной теоремы арифметики следует, что все делители числа п можно записать в виде

где

Из этой теоремы также вытекает и второй способ нахождения НОД и НОК. Предположим, что числа а и b представлены в виде:

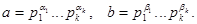
Здесь к каноническому представлению числа а приписаны в нулевой степени те простые числа, которые входят в каноническое представление числа b, но не входят в представление числа а. Соответственно то же проделано с каноническим представлением числа b. Тогда

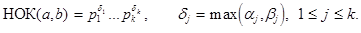
Дата добавления: 2015-10-23