
Читайте также:
|
Рассмотрим множество C всех пар действительных чисел  Для них введем отношение равенства и действия сложения и умножения:
Для них введем отношение равенства и действия сложения и умножения:
 (1)
(1)
 (2)
(2)
 (3)
(3)
Например,




Отождествим пару (а, 0) с числом а. Это отождествление оправдано в силу согласования введенных действий с действиями над вещественными числами:


Можно заметить, что
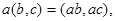
и что пара (0,1) обладает удивительным свойством:

Для этой пары принято обозначение:  (от французского слова imaginare) и называется она мнимой, т.е. воображаемой единицей. В новых обозначениях данное свойство можно переписать так:
(от французского слова imaginare) и называется она мнимой, т.е. воображаемой единицей. В новых обозначениях данное свойство можно переписать так:
 (4)
(4)
Для пары  имеем
имеем  т.е.
т.е.
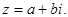 (5)
(5)
Множество С называется множеством комплексных чисел, а выражение  называется алгебраической формой записи комплексного числа. При b = 0 комплексное число
называется алгебраической формой записи комплексного числа. При b = 0 комплексное число  является действительным числом а, т.е.
является действительным числом а, т.е. 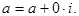 Это означает, что мы получили расширение множества действительных чисел, в котором уравнение
Это означает, что мы получили расширение множества действительных чисел, в котором уравнение  разрешимо, имеет корень i. Легко увидеть, что отношение равенства, сложение и умножение, а также вычитание и деление запишутся в следующем виде:
разрешимо, имеет корень i. Легко увидеть, что отношение равенства, сложение и умножение, а также вычитание и деление запишутся в следующем виде:
 (6)
(6)
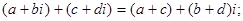 (7)
(7)
 (8)
(8)
 (9)
(9)
 где
где  (10)
(10)
Заметим, что понятия "больше" и "меньше" для комплексных чисел не определяются, т.е. говорить о том, что одно комплексное число больше или меньше другого, нельзя, это лишено смысла.
Вычитание вводится как действие обратное сложению. Разностью 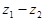 чисел
чисел  называется такое число
называется такое число  , для которого
, для которого 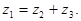 Легко доказать, что разность двух комплексных чисел всегда существует и единственная.
Легко доказать, что разность двух комплексных чисел всегда существует и единственная.
Деление вводится как действие, обратное умножению. Частным  чисел
чисел  и
и  называется такое число
называется такое число  для которого
для которого 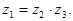 Частное существует и единственно всегда, когда делитель
Частное существует и единственно всегда, когда делитель 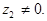 В практических вычислениях обычно не пользуются формулой (10), а поступают так:
В практических вычислениях обычно не пользуются формулой (10), а поступают так:

Свойства арифметических операций:
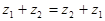 – коммутативность сложения;
– коммутативность сложения;
 – ассоциативность сложения;
– ассоциативность сложения;
 – коммутативность умножения;
– коммутативность умножения;
 – ассоциативность умножения;
– ассоциативность умножения;
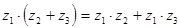 – дистрибутивность умножения относительно сложения слева.
– дистрибутивность умножения относительно сложения слева.
Все эти свойства легко доказать, используя аналогичные свойства действительных чисел. Следовательно, арифметические действия над комплексными числами можно проводить по правилам действительных чисел, лишь заменяя i 2 на -1 и объединяя отдельно члены, содержащие i и не содержащие i. Числа а и b называют соответственно действительной и мнимой частью комплексного числа 
Пример. Даны комплексные числа 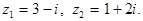 Найти: а) сумму
Найти: а) сумму  б) разность
б) разность  в) произведение
в) произведение  г) частное
г) частное 
Решение:
а) 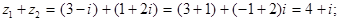
б) 
в) 
г) 
Пример. Записать в алгебраической форме число 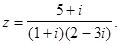
Решение: 
Дата добавления: 2015-10-23; просмотров: 153 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Упражнения и задачи | | | Геометрическая интерпретация комплексных чисел |