
Читайте также:
|
Число 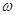 называется корнем п-ой степени из комплексного числа z, если
называется корнем п-ой степени из комплексного числа z, если 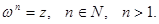 Например, числа - i, i являются корнями второй степени из числа -1, так как
Например, числа - i, i являются корнями второй степени из числа -1, так как 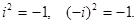 Если z = 0, то
Если z = 0, то 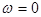 – единственный корень п -ой степени.
– единственный корень п -ой степени.
Теорема. Для любого комплексного числа  существует ровно п корней п -ой степени, которые определяются по формуле:
существует ровно п корней п -ой степени, которые определяются по формуле:

Доказательство: Пусть 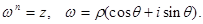 Тогда
Тогда

Отсюда
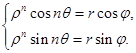
Возведя обе части каждого равенства в квадрат и сложив полученные равенства, получим:
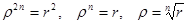 (арифметический корень).
(арифметический корень).
Из условия 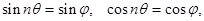 имеем
имеем
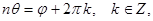
т.е.
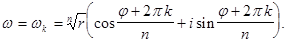 ■
■
Для k = 0, 1, 2, 3,..., п -1 получаются различные значения чисел 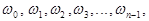 а для каждого из остальных значений
а для каждого из остальных значений 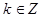 будет получаться одно из этих чисел.
будет получаться одно из этих чисел.
Отсюда следует, что все числа  имеют равные модули
имеют равные модули 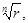 но различные главные аргументы, отличающиеся друг от друга на величину
но различные главные аргументы, отличающиеся друг от друга на величину 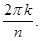 Числа
Числа  , следовательно, соответствуют точкам комплексной плоскости, расположенным в вершинах правильного п -угольника, вписанного в круг радиуса
, следовательно, соответствуют точкам комплексной плоскости, расположенным в вершинах правильного п -угольника, вписанного в круг радиуса 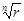 с центром в начале координат.
с центром в начале координат.
Пример. Найти все корни четвертой степени из числа 16 i.
Решение: Поскольку 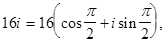 то применяя формулу для извлечения корней, получаем
то применяя формулу для извлечения корней, получаем

Следовательно,
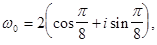
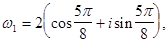
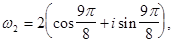

Пример. Вычислить 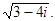
Решение: Пусть 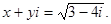 Тогда
Тогда 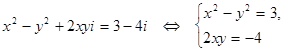
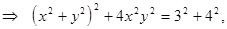 т.е.
т.е. 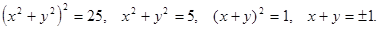 Если
Если 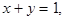 то
то 
 Если
Если 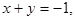 то
то 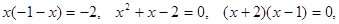
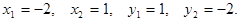
Ответ: 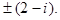
Упражнения и задачи
Вычислить квадратные корни из чисел:
а) 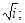 б)
б) 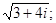 в)
в) 
Найти все значения следующих корней:
а) 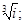 б)
б) 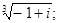 в)
в) 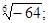 г)
г) 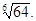
Найти:
а) 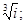 б)
б) 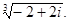
Решить уравнение:
а) 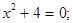 б)
б)  в)
в) 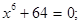 г)
г) 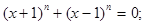 д)
д) 
Корни из 1
По формулам извлечения корней все п корней п -ой степени из 1 можно записать в виде:

т.е. все они являются степенями одного корня
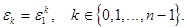
Теорема. Множество 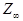 всех корней из 1 образуют мультипликативную группу.
всех корней из 1 образуют мультипликативную группу.
Доказательство: Пусть 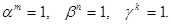 Тогда
Тогда 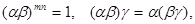 т.е. множество
т.е. множество 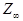 замкнуто относительно умножения, выполняется и аксиома ассоциативности (она выполняется для всех комплексных чисел, а, следовательно, и для корней из 1). Так как
замкнуто относительно умножения, выполняется и аксиома ассоциативности (она выполняется для всех комплексных чисел, а, следовательно, и для корней из 1). Так как 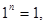 то это множество содержит нейтральный элемент относительно умножения. Ясно, что если
то это множество содержит нейтральный элемент относительно умножения. Ясно, что если 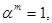 то
то 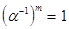 также, т.е. для любого элемента
также, т.е. для любого элемента  из
из 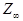 элемент
элемент  тоже принадлежит этому множеству. ■
тоже принадлежит этому множеству. ■
Теорема. Множество  всех корней п -ой степени из 1 образуют конечную мультипликативную группу.
всех корней п -ой степени из 1 образуют конечную мультипликативную группу.
Доказывается аналогично предыдущей теореме. ■
Пример. Найти все корни третьей степени из 1.
Решение: 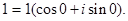 Поэтому
Поэтому
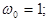
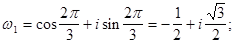
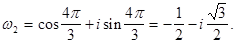
Все корни п -ой степени из 1 изображаются точками, лежащими на окружности радиуса 1 с центром в О и делящими эту окружность на п равных частей.
Пример. Доказать тождество 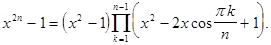
Доказательство: 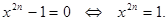 Это уравнение имеет
Это уравнение имеет  корней, корней из 1, т.е. его корни:
корней, корней из 1, т.е. его корни:
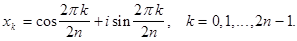
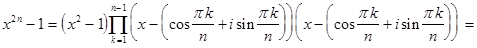

Пример. Найти сумму всех корней п -ой степени из 1.
Решение: Пусть 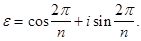 Тогда все корни п -ой степени из 1 можно представить в виде
Тогда все корни п -ой степени из 1 можно представить в виде 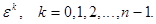 Отсюда сумма всех корней равна
Отсюда сумма всех корней равна
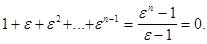
Ответ: 0.
Пример. Найти произведение всех корней п -ой степени из 1.
Решение: Разобьем все сомножители, отличные от 1 и -1, на пары взаимно обратных чисел. Произведение чисел каждой пары равно 1. Если п четно, то все произведение равно 1, а если п нечетно, то -1.
Ответ: 
Дата добавления: 2015-10-23; просмотров: 234 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Упражнения и задачи | | | Упражнения и задачи |