Алгоритм De Boor для Кривых NURBS

Алгоритм De Boor также работает для кривых NURBS. Просто умножаем каждую контр. точку на ее вес, преобразуя тем самым кривую NURBS в 4х-мерный B-spline, проводим вычисления по алгоритму de Boor над этой кривой B-spline, и затем проецируем ее обратно на 3D - пространство при помощи деления первых трех координат на четвертую.

Основные Понятия

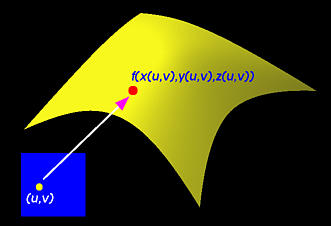
Есть два типа поверхностей, обычно использующихся в системах моделирования, - это параметрические и неявные. Параметрические поверхности определяются набором трех функций, по одной на каждую координату:

f (u, v) = (x (u, v), y (u, v), z (u, v)),

где параметры u и v находятся в определенных границах. Для нашей цели мы будем брать значения u и v в пределах от 0 до 1. Таким образом, (u, v) - это точка в квадрате, определяемом точками (0,0), (1,0), (0,1) и (1,1) на коорд. плоскости uv. Следующий рисунок иллюстрирует это понятие.

Неявные поверхности, с другой стороны, определяются многочленом с тремя переменными:

p (x, y, z) = 0

Как и в случае с кривыми, если x (u, v), y (u, v) и z (u, v) - это многочлены, то параметрические поверхности не смогут описывать многие поверхности, которые могут быть описаны в неявном виде. Хороший пример - сфера. Можно легко проверить этот факт с помощью доказательства, использовавшегося в случае с окружностями. Если x (u, v), y (u, v) и z (u, v) - это рациональные многочлены (т.e. частное двух многочленов), то параметрические поверхности могут описывать сферы, эллипсоиды и многие другие поверхности. Тем не менее, как и кривые, многие неявные поверхности не имеют параметрической формы. Образно говоря, неявные поверхности "сильнее" параметрических.

Вот несколько технических терминов. Поверхности, имеющие вид многочлена (неявные) называются алгебраическими поверхностями. Высшая степень из всех членов многочлена - это степень алгебраической поверхности. Таким образом, сферы и все квадратичные поверхности - это алгебраические поверхности второй степени, а, например, тор - это алгебр. поверхность 4 степени. Далее показана алгебр. пов-ть 3 степени, неявное уравнение которой

8 x ² - xy ² + xz ² + y ² + z ² - 8 = 0:

Некоторые алгебр. пов-ти имеют рациональные параметрические формы, например, сферы и все квадратичные поверхности. Этот тип алгебраич. поверхностей называют рациональными алгебраическими поверхностями. Теоретически, если дана алгебраич. поверхность в рациональной параметрической форме, всегда можно избавиться от параметров u и v, чтобы результат был в неявном виде. Этот процесс (перевод из параметрического вида в неявный) называют имплиситизацией (гы гы. Ну как словечко? хе хе - прим. перев.) (implicitization). Тем не менее, не все алебраические поверхности являются рациональными. К сожалению, проверить, является ли алгебраическая поверхность рациональной, очень сложно, не смотря на то, что у алгебраической геометрии такие определяющие теоремы. С вычислительной точки зрения это невыполнимо.

Дата добавления: 2015-10-29