Важные Свойства Кривых NURBS

Далее перечисляются важные свойства кривых NURBS. Пожалуйста, сравните их со свойствами кривых B-spline. Заметьте, что NURBS могут быть открытыми, фиксированными и замкнутыми. Как и с кривыми B-spline, если первые p +1 и последние p +1 узлов равны левой и правой границам области определения, кривая называется фиксированной.

1. Кривая NURBS p(u) - это кусочная кривая, каждый компонент которой - это рациональная кривая степени p
2. Равенство m = n + p + 1 должно выполняться
3. Фиксированная кривая NURBS p(u) проходит через две крайние контр. точки p₀ и p _n
4. Свойство Сильного Огранич. Многоугольника: кривая NURBS содержится в огранич. многоугольнике ее контр. точек. Более того, если u находится на интервале [ u_i, u_{i +1}), то p(u) находится в огр. многоугольнике контр. точек p _i-p, p _{i-p +1},..., p _i
   Мы очень ясно покзали, что все весы должны быть неотрицательными. Если некоторые из них отрицательны, то свойство сильного огранич. многоугольника, а может быть, даже просто огранич. многоугольника, не будет выполняться. Далее, на рисунке слева показана кривая NURBS 2 степени с n = 2, m = 5 и фиксированными тремя первыми и последними узлами. Весы контр. точек на обоих концах равны 1, а вес средней контр. точки равен 0.5. Получается эллиптическая дуга. Отрезок кривой лежит в огранич. многоугольнике.

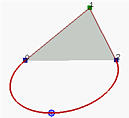
На среднем рисунке вес средней точки равен нулю. Так как эта контр. точка не имеет эффекта, то результат - это отрезок прямой с концами в крайних точках. Он также лежит внутри огранич. многоугольника.

Если вес сделать равным -0.5, отрезок кривой не будет лежать внутри огранич. многоугольника, поэтому свойство не будет выполняться.

1. Схема Локального Изменения: измененние положения контр. точки p _i влияет на кривую p(u) только на интервале [ u_i, u_{i+p +1})
   Это следует из свойства локального изменения базисных функций кривых B-spline. Вспомните, что R_i,p (u) не равно нулю на интервале [ u_i, u_{i+p +1}). Если u не лежит на этом интервале, так как R_i,p (u) равно нулю и R_i,p (u) p _i не влияет на вычисление p (u). С другой стороны, если u находится в указанном интервале, R_i,p (u) не равно нулю и, если R_i,p (u) p _i изменить, то изменится и p (u).

Эта схема локального изменения очень важна для разработки кривых, потому что мы можем менять кривую локально, без изменения формы кривой в целом. Более того, если нужно точное изменение кривой, можно ввести побольше узлов (а значит, и контр. точек) так, чтобы нужная область сжалась до более узкой. Мы поговорим о введении узлов позже.

1. p(u) является C^p-k -непрерывной в узле с множественностью k
   Если u не является узлом, то p (u) лежит в середине криволинейного отрезка степени p и поэтому является бесконечно дифференцируемой. Если u - это узел в ненулевой области определения R_i,p (u), то из-за того, что R_i,p (u) только C^p-k -непрерывна, то то же самое и с p (u).
2. Свойство Уменьшения Изменчивости:
   Свойство уменьшения изменчивости также подходит для кривых NURBS. Если кривая находится в плоскости (соотв., в пространстве), то это значит, что не существует прямой, (соотв., плоскости), пересекающей эту кривую в большем количестве мест, чем ее контр. ломаную.
3. Кривые B-spline и Кривые Безье - это Особые Случаи Кривых NURBS.
   Если все весы равны, кривая NURBS становится кривой B-spline. Если к тому же n = p (т.e. степень кривой B-spline равна n, количество контр. точек минус 1) и всего 2(p + 1) = 2(n + 1) узлов, p + 1 из которых фиксированы на обоих концах, то эта кривая NURBS вырождается в кривую Безье.
4. Проекционная Инвариантность [Invariance]
   Если к кривой NURBS применяются проекционные преобразования, то результат можно получить из проекционных преобразований контр. точек. Это полезное свойство. В общем, почти то же самое, что и в случае с кривыми B-spline и Безье.

Заметьте, что кривые Безье и B-spline удовлетворяют только свойству инвариантности преобразований подобия в отличие от проекционных преобразований. Это из-за того, что только кривые NURBS поддерживают проекционные преобразования.

Дата добавления: 2015-10-29