B-spline: Мотивация

Допустим, нам нужно спроектировать профиль вазы. Рисунок слева - это кривая Безье 11 степени; но все-же сложно сделать так, чтобы "шея" огибала отрезок p ₄ p ₅. Конечно, можно добавить контрольных точек около этого отрезка, чтобы увеличить вес в этой области. Но тогда увеличится степень кривой. Во многих случаях невыгодно использовать кривые высших степеней.

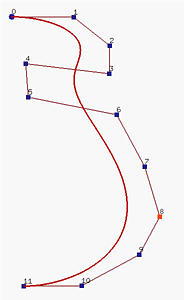
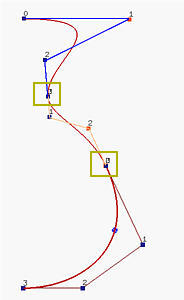
Как оговаривалось на предыдущей странице о производных кривых Безье, мы можем объединить две кривых Безье. Если последний сегмент ломаной первой кривой и первый сегмент ломаной второй кривой лежат на одной прямой, получаем по крайней мере G ¹-непрерывность, так как касательные векторы направлены в одну сторону (т.e., если их длины равны, получаем непрерывность C ¹). Рисунок посередине показывает это. На нем три отрезка кривых Безье, точки соединения показаны в желтых прямоугольниках. Мы видим, что с помощью нескольких кривых Безье меньших степеней, удовлетворяющих условию "коллинеарности", можно получить необходимую сложную форму. Но поддержание этой "коллинеарности" может быть довольно утомительным и нежелательным.

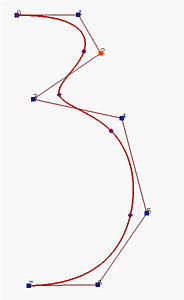
Возможно ли использовать отрезки кривых младших степеней, не заботясь об этом условии "коллинеарности"? Кривые B-spline - это обобщение кривых Безье, разработанные для такого случая. На правом рисунке изображена кривая B-spline третьей степени с 8-ю контрольными точками. Фактически, это - пять кривых Безье 3-й степени, вместе образующих кривую B-spline, определяемую контрольными точками. Маленькие точки делят кривую на отрезки. Можно перемещать контрольные точки, чтобы изменить форму кривой, также, как и с кривыми Безье. Также можно изменять деление кривой. Таким образом, кривые B-spline имеют большую степень свободы в проектировании кривых.

Деление кривой напрямую довольно сложно. Вместо этого мы можем разделить диапазон кривой. То есть, если область кривой - это [0,1], то этот закрытый диапазон разделяется точками, называемыми узлами. Пусть узлы будут 0 <= u ₀ <= u ₁ <=... <= u_m <= 1. Тогда точки p (u_i) делят кривую, как показано на рисунке ниже, и, следовательно, изменение деления отрезка [0,1] изменяет форму кривой.

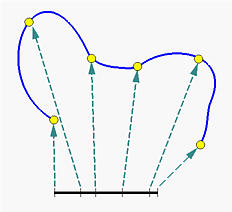
В итоге, чтобы создать кривую B-spline, нам нужны: набор контрольных точек, набор узлов и набор коэффициентов, по одному на каждую контрольную точку, т.е. чтобы все отрезки кривой соединялись и выполненялось нужное условие непрерывности. Вычисление коэффициентов - это, возможно, самая сложная часть работы, так как они должны гарантировать выполнение определенных условий непрерывности. К счастью, эти вычисления в этом курсе не понадобятся. Нам лишь нужно знать их характеристики для рассуждения о кривых B-spline.

Дата добавления: 2015-10-29