Кривые B-spline: Перемещение Контрольных Точек

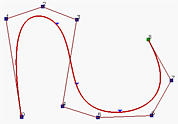
Перемещение контрольных точек - самый очевидный способ изменения формы кривой B-spline. Схема локального изменения, обсуждавшаяся ранее, говорит о том, что изменение позиции контр. точки p_i влияет на кривую p(u) только на промежутке [u_i, u_i+p+1), где p - это степень кривой B-spline. Фактически, измененние формы является переместительным в направлении смещенной контр. точки. Говоря точнее, если контр. точка p_i сместилась в каком-то направлении а новое положение q_i, то точка p(u), где u лежит на [u_i, u_i+p+1), сместится в том же направлении от p_i до q_i. Тем не менее, расстояние смещения различается среди разных точек. На следующих рисунках, контр. точка p₄ перемещается из положения на первом рисунке в новое положение, показанное на среднем рисунке, и затем в конечное положение (правый рисунок). Как видите, точки, соответствующие узлам (помечены тпеугольниками), перемещаются в том же направлении.

Давайте присмотримся детальнее. Допустим, p(u) - это данная кривая B-spline степени p, определяемая как

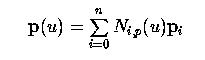
Пусть контр. точка p_i перемещается в новое положение p_i + v. Тогда новая кривая B-spline степени p имеет вид:

Таким образом, новая кривая C(u) - это просто сумма исходной кривой p(u) и вектора переноса N_i,p(u)v. Так как N_i,p(u) не равно нулю на интервале [u_i,u_i+p+1), то, если u не на этом интервале, то член выражения, отвечающий за перенос, равняется нулю и не влияет на форму кривой. Таким образом, для кривых B-spline, перемещение контр. точки влияет только на форму одной секции. Изображенная ниже кривая слева - это кривая B-spline 4 степени (т.e. p = 4), построенная по 13 контр. точкам (т.e. n = 12) и 18 узлам (т.e. m = 17). Эти 18 узлов являются простыми и описывают фиксированную кривую (т.e., u₀ = u₁ = u₂ = u₃ = u₄ = 0 и u₁₃ = u₁₄ = u₁₅ = u₁₆ = u₁₇ = 1). Остальные узлы образуют 9 узловых интервалов, и, следовательно, 9 отрезков кривой, как показано на рисунке. Эти девять узловых интервалов и отрезков кривой обозначены так:

Интервал	[u4,u5)	[u5,u6)	[u6,u7)	[u7,u8)	[u8,u9)	[u9,u10)	[u10,u11)	[u11,u12)	[u12,u13)
Отрезок

Теперь давайте переместим p₆. Результат показан на рисунке справа. Как видите, кривая сместилась в том же направлении, что и контр. точка p₆. Коэффициент при p₆ - это N_6,4(u), а это не равно нулю на [u₆, u₁₁). Таким образом, перемещение p₆ влияет на отрезки кривой 3, 4, 5, 6 и 7. Отрезки 1, 2, 8 и 9 остаются неизменными.

Дата добавления: 2015-10-29