Базисные Функции B-spline: Определение

Базисные функции Безье использовались в качестве весов. Базисные функции B-spline будут использоваться так же; тем не менее, они гораздо более сложны. Есть два интересных свойства, которые не являются частью базисных функций Безье, а именно: (1) интервал разделяется узлами, и (2) базисные функции не являются ненулевыми на всем интервале. Фактически, каждая базисная функция B-spline является ненулевой на нескольких смежных под-интервалах и, в итоге, базисные функции B-spline являются вполне "локальными".

Пусть U - это последовательность m + 1 неубывающих действительных чисел, u ₀ <= u ₂ <= u ₃ <=... <= u_m. Числа u_i называются узлами, последовательность U - узловым вектором, а полуоткрытый интервал [ u_i, u_{i +1}) - i-м узловым диапазоном. Заметьте, так как некоторые u_i могут быть равны, то соответствующих узловых диапазонов может не существовать. Если узел u_i появляется k раз (i.e., u _i = u_{i +1} =... = u_{i+k -1}), где k > 1, u_i называется множественным узлом k -й множественности, пишется u_i (k). Иначе, если u_i появляется лишь однажды, это - простой узел. Если узлы равномерно разделены (т.e. u_{i +1} - u_i постоянно для 0 <= i <= m - 1), узловой вектор или последовательность узлов называется однородной(-ым); иначе, неоднородной.

Узлы можно представить как точки, делящие интервал [ u ₀, u_m ] на узловые интервалы. Все базисные функции B-spline должны иметь область определения на [ u ₀, u_m ]. Таким образом, используем u ₀ = 0 и u_m = 1, чтобы преобразовать интервал в [0,1].

Чтобы описать базисные функции B-spline, нужен еще один параметр, степень этих базисных функций, p. i -я базисная функция B-spline степени p (пишется N_i,p (u)), описывается рекурсивно:

Вышеуказанное уравнение обычно называют рекурсивной формулой Cox - de Boor. Это определение выглядит сложным. Но оно просто для понимания. Если степень равна нулю (т.e., p = 0), эти базисные функции являются скачковыми и это как раз то, о чем говорит первое выражение в формуле. То есть, базисная функция N_{i ,0}(u) равна 1, если u лежит на i -м узловом интервале [ u_i, u_{i +1}). Например, если есть четыре узла u ₀ = 0, u ₁ = 1, u ₂ = 2 и u ₃ = 3, узловые интервалы 0, 1 и 2 - это [0,1), [1,2), [2,3) и базисные функции 0 степени - это N _0,0(u) = 1 на [0,1) и 0 в других случаях, N _1,0(u) = 1 на [1,2) и 0 в других случаях, и N _2,0(u) = 1 на [2,3) и 0 в других случаях. Это показано ниже:

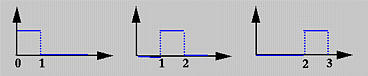
Чтобы понять принцип расчета N_i,p (u) для p больше 0, вернемся к треуголной схеме расчета. Все узловые интервалы - в левом (первом) столбце, а все базисные функции нулевой степени - во втором. Это показано на следующей диаграмме.

Чтобы вычислить N_{i ,1}(u), нужно N_{i ,0}(u) и N_{i +1,0}(u). Таким образом, мы можем вычислить N _0,1(u), N _1,1(u), N _2,1(u), N _3,1(u) и так далее. Все эти N_{i ,1}(u) записываются в третий столбец. Когда будут найдены N_{i ,1}(u), можно будет вычислить N_{i ,2}(u) и записать их в четвертый столбец. Продолжаем в том же духе, пока не вычислим все нужные N_{i , p} (u).

Выше мы нашли N _0,0(u), N _1,0(u) и N _2,0(u) для узлового вектора U = { 0, 1, 2, 3 }. Давайте вычислим N _0,1(u) и N _1,1(u). Чтобы вычислить N _0,1(u), так как i = 0 и p = 1, по определению имеем

N _0,1(u) = (u - u ₀) / (u ₁ - u ₀) N _0,0(u) + (u ₂ - u) / (u ₂ - u ₁) N _1,0(u)

Так как u ₀ = 0, u ₁ = 1 и u ₂ = 2, вышеизложенное преобразуется к виду

N _0,1(u) = u N _0,0(u) + (2 - u) N _1,0(u)

Так как N _0,0(u) не равно нулю на [0,1), а N _1,0(u) не равно нулю на [1,2), когда u лежит на [0,1) (соотв., на [1,2)), только N _0,0(u) (соотв., N _1,0(u)) влияет на [? contributes to] N _0,1(u). Таким образом, когда u в пределах [0,1), N _0,1(u) равно uN _0,0(u) = u, а когда u в пределах [1,2), N _0,1(u) равно (2 - u) N _1,0(u) = (2 - u). Простые вычисления дают N _1,1(u) = u - 1, если u лежит на [1,2), а N _1,1(u) = 3 - u, если u лежит на [2,3). На следующем рисунке черные и красные линии - это соответственно N _0,1(u) и N _1,1(u). Заметьте, что N _0,1(u) (соотв., N _1,1(u)) не равно нулю на [0,1) и [1,2) (соотв., на [1,2) и [2,3)).

Как только будут найдены N _0,1(u) и N _1,1(u), можно вычислить N _0,2(u). Из определения следует:

N _0,2(u) = (u - u ₀) / (u ₂ - u ₀) N _0,1(u) + (u ₃ - u) / (u ₃ - u ₁) N _1,1(u)

Подставляя эти значения узлов, имеем

N _0,2(u) = 0.5 u N _0,1(u) + 0.5 (3 - u) N _1,1(u)

Заметьте, что N _0,1(u) не равно нулю на [0,1) и [1,2), а N _1,1(u) не равно нулю на [1,2) и [2,3). Таким образом, имеем три случая:

1. u в пределах [0,1):
   В этом случае, только N _0,1(u) влияет на значение N _0,2(u). Так как N _0,1(u) равно [is] u, имеем

N _0,2(u) = 0.5 u ².

1. u в пределах [1,2):
   В этом случае, и N _0,1(u), и N _1,1(u) влияют на N _0,2(u). Так как на [1,2), N _0,1(u) = 2 - u и N _1,1(u) = u - 1, имеем

N _0,2(u) = (0.5 u)(2 - u) + 0.5(3 - u)(3 - u) = 0.5(-3 + 6 u - 2 u ²)

1. u в пределах [2,3):
   В этом случае, только N _1,1(u) влияет на N _0,2(u). Так как N _1,1(u) = 3 - u на [2,3), имеем

N _0,2(u) = 0.5(3 - u)(3 - u) = 0.5(3 - u)²

Если нарисовать отрезок кривой для каждого из трех случаев, то станет видно, что два смежных отрезка кривых соединяются, образуя кривую по узлам. Говоря точнее, отрезки первого и второго случаев соединяются при u = 1, а второго и третьего случаев - при u = 2. Это показано на рисунке ниже. Заметьте, что образованная кривая, изображенная на рисунке, является гладкой. Но в общем случае это не так, если, например, мы имеем дело с множественными узлами.

Дата добавления: 2015-10-29