Соотношение Между Производной и Алгоритмом de Casteljau

Перепишем производную кривой Безье, разбив последний член p _{i +1}- p _i на два:

Таким образом, производная кривой Безье - это разность двух кривых Безье степени n -1. Для простоты, пусть эти кривые будут C ₁(u) и C ₂(u):

Из этих определений получаем, что первая кривая C ₁(u) описывается контрольными точками p ₁, p ₂,..., p _n, а вторая кривая C ₂(u) описывается контрольными точками p ₀, p ₁,..., p _{n -1}. Производная равна:

Таким образом, теоретически, для того, чтобы вычислить производную p (u) для отдельного u, можно использовать алгоритм de Casteljau, чтобы вычислить C ₁(u) и C ₂(u). Затем, вычислив их разность и умножив на n, получим p '(u).

Теперь надо использовать алгоритм de Casteljau. Посмотрите на рисунок ниже. В левом столбце находятся все данные контрольные точки. Точка n0 дает точку p (u) на кривой, а отрезок, соединяющий (n-1)0 и (n-1)1 - это последняя ломаная в алгоритме de Casteljau. Фактически, n0 лежит на отрезке от (n-1)0 до (n-1)1, причем отношение расстояний между (n-1)0 и n0, и между (n-1)0 и (n-1)1 равно u.

Так как кривая C ₁(u) описывается контрольными точками 01, 02,..., 0n, то, используя диаграмму (выше), можно видеть, что (n-1)1 - это точка на кривой C ₁(u). Соответственно, так как C ₂(u) описывается контрольными точками 00, 01,..., 0(n-1), видно, что (n-1)0 - это точка на кривой C ₂(u). Таким образом, вектор C ₁(u)- C ₂(u) - это вектор от точки (n-1)0 до точки (n-1)1, а производная p (u) равна C ₁(u)- C ₂(u), умноженному на n.

Что из этого следует? Так как ломаная от (n-1)0 до (n-1)1 в алгоритме de Casteljau имеет то же направление, что и касательный вектор в точке p (u), она касательна кривой в p (u)! В итоге получаем, что

Последняя кривая, т.е. отрезок, в алгоритме de Casteljau, касательна кривой Безье в точке p(u).

Пример на следующем рисунке поясняет это. Показана точка, для которой u = 0.5. Видно, что последний отрезок в сети de Casteljau касателен кривой в p (0.5).

Производные Высших Порядков [Higher Derivatives]

Вычисление производных высших порядков кривых Безье - дело несложное. Вспомним, что производная p (u) - это

Применяя формулу производной к этой кривой Безье, получим следующее, т.е. вторую производную исходной кривой:

Найдя p '(u) и p ''(u), можно будет очень легко найти направляющую тройку веторов и кривизну в точке p (u). Производные высших порядков можно находить, рекурсивно применяя формулу производной.

Чтобы подробнее рассмотреть производные высших порядков, нужно ввести понятие конечной разности. Пусть конечная разность нулевого уровня D _i ⁰ описывается контрольными точками P _i для 0 <= i <= n. Затем, конечная разность первого уровня D _i ¹ - это разность между элементами предыдущего уровня, т.е. нулевого (D _i ⁰):

Заметьте, что в разности первого уровня только n точек, на одну меньше, чем количество исходных контрольных точек. Еще точнее, первый уровень разности - это

Второй уровень разности описывается разностью точек первого уровня.

Второй уровень разности имеет n -1 точек. Повторяя эту процедуру, можно получить k -й уровень разности (см. ниже). В k -ом уровне разности n-k +1 точек.

С помощью такого обозначения можно описать производную довольно коротко. Прежде всего, перепишем p '(u) используя разности D _i ¹:

Вычисляя производную p '(u), чтобы получить p ''(u), получим формулу p ''(u) с участием D _i ²:

Сделав то же самое с p ''(u), получим формулу p '''(u) через D _i ³:

Продолжая в том же духе, можно получить k -ю производную p ^{[ k ]}(u) через D _i ^k:

Таким образом, чтобы вычислить k -ю производную p (u) для конкретного u, можно сначала вычислить разности D _i^k и применить алгоритм de Casteljau для нахождения точки, соответствующей u на кривой Безье, описываемой точками D _i^k. Говоря точнее, можно сгруппировать все D _i ⁰ в нулевой столбец, назначить стрелкам знаки (вверх (красные) +, вниз (синие) -) для вычисления столбца 1 разностей D _i ¹. Повторяем эту операцию до тех пор, пока не дойдем до столбца k, как показано ниже:

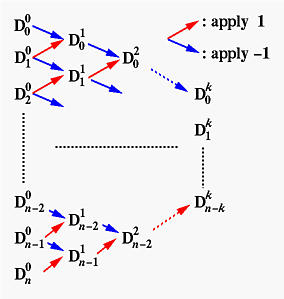
В конце концов, применив алгоритм de Casteljau к точкам столбца k при данном u, получим вектор p ^{[ k ]}(u)!

Дата добавления: 2015-10-29