Почему Направляющая Тройка Важна?

Направляющая тройка векторов - это не только математическое понятие. Оно также дает важную информацию о движущемся объекте. Например, в полете самолет движется по кривой. То есть, он движется по направлению касательного вектора, вектор "вверх" направлен по бинормальному вектору, а показатель и направление поворота - это соответственно кривизна и направление нормального вектора.

Есть еще такой показатель, как кручение, он мы его тут обсуждать не будем. Нафиг надо... Неохота.

Вопросы Непрерывности

Как и упоминалось ранее, грани и ребра могут быть не только отрезками и многоугольниками, но и соответственно отрезками кривых и элементами поверхностей. Вот тут-то и могут появиться проблемы. На рисунке показаны две поверхности, соединяющиеся по кривой. Два отрезка кривых, показаны желтым и белым, соединяются в вершине X. Пусть эти кривые заданы уравнениями f (u) и g (v), где u и v - в интервалах [ a, b ] и [ m, n ] соответственно. Проблема в том, как проверить, сходятся ли они "гладко".

Возьмем "правый" конец отрезка кривой f (b) и "левый" конец отрезка кривой g (m). Если f (b) и g (m) равны, как, например, на рисунке, говорят, что кривые f () и g () C ⁰ непрерывны в точке f (b)= g (m). Если для всех i <= k i -ые производные в точках f (b) и g (m) равны, говорят, что кривые C^k непрерывны в точке f (b)= g (m).

Прямо из определения следует, что, если два отрезка кривых C^k непрерывны в f (b)= g (m), они также Cⁱ непрерывны для всех i <= k. С другой стороны, если k -ые производные двух кривых в точке соединения не равны, они не могут быть Cⁱ непрерывными для любых i >= k.

Вот простой пример. Кривая состоит из двух отрезков парабол:

f (u) = (u, - u ², 0)
g (v) = (v, v ², 0),

где f (), кривая слева, и g (), кривая справа, соответственно в пределах [-1,0] и [0,1]. Проверим, являются ли эти отрезки кривых C ² непрерывными в начале координат.

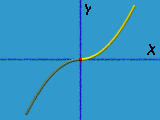
Вот инфа, необходимая для такой проверки:

f '(u) = (1, -2 u, 0)
f ''(u) = (0, -2, 0)
g '(v) = (1, 2 v, 0)
g ''(v) = (0, 2, 0)

Так как f '(0) = g '(0) = (1, 0, 0), эти кривые C ¹ непрерывны в начале координат. Тем не менее, так как f ''(0) = (0, -2, 0) не равно g ''(v) = (0, 2, 0), они не являются C ² непрерывными в начале координат. f ''(u) направлено вниз, а g ''(u) - вверх и оба постоянны, т.е. не зависят от u и v. Таким образом, при переходе точки через начало координат - от зеленого к желтому отрезку, вторая производная резко меняет свое направление. Получается, что эти отрезки кривых не являются C ² непрерывными в начале координат.

Найдем выражения для их кривизны:

Кривизна f (u) = 2/(1 + 4 u ²)^1.5
Кривизна g (v) = 2/(1 + 4 v ²)^1.5

Они имеют одинаковый вид, хотя u на отрезке [-1,0], а v - на отрезке [0,1]. Фактически, кривизна этих двух криволинейных отрезков от одной и той же кривой и, следовательно, они непрерывны по кривизне в точке соединения (т.e., f (0)= g (0))! Получается, кривые могут быть C ¹ непрерывными и даже непрерывными по кривизне, но в то же время не C ² непрерывными.

Дата добавления: 2015-10-29