Проблемы с Параметрическим Представлением

C^k непрерывность кажется удобным инструментом для проверки на гладкость соединения кривых. Но и тут есть проблема. Пусть даны следующие отрезки кривых:

f (u) = A + u (B - A)
g (v) = B + v (C - B),

где A, B и C - три коллинеарные (лежащие на одной прямой) точки, как показано на рисунке.

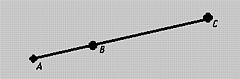
Когда u (соотв., v) изменяется от 0 до 1, f (u) (соотв., g (v)) пробегает от A до B (соотв., от B до C). Отрезки f (u) и g (v), очевидно, C ⁰ непрерывны в точке соединения B. А C ¹ непрерывны ли они?

f '(u) = B - A
g '(v) = C - B

Таким образом, f '(u) = B - A в общем случае не равно g '(v) = C - B и, следовательно, два этих отрезка не C ¹ непрерывны в точке соединения B!

Странно? Это все из-за параметризации. Если заменить направляющие векторы B - A и C - B на единичные векторы и изменить интервалы параметров u и v, проблема пропадет. Таким образом, уравнения нужно изменить на следующие:

F (u) = A + u (B - A)/ | B - A |
G (v) = B + v (C - B)/ | C - B |,

где u в пределах от 0 до | B - A |, а v в пределах от 0 до | C - B |. Теперь, так как мы имеем F '(u) = G '(v) = единичному вектору в направлении от A до C, отрезки C ¹ непрерывны. То есть, параметризация отрезков кривых - хорошая вещь 8).

Вот еще один пример, здесь PI равно 3.1415926, u и v в границах [0,1].

f (u) = (-cos(u ² PI/2), sin(u ² PI/2), 0)
g (v) = (sin(v ² PI/2), cos(v ² PI/2), 0)

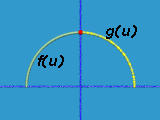
Когда u изменяется от 0 до 1, f (u) проходит левую часть полукруга. Аналогично с правой частью. Они соединяются в точке, показаной красным, (0,1,0) = f (1) = g (0). Имеем следующее:

f '(u) = (PI u sin(u ² PI/2), PI u cos(u ² PI/2), 0)
f ''(u) = (PI² u ² cos(u ² PI/2), -PI² u ² sin(u ² PI/2), 0)
f '(u) × f ''(u) = (0, 0, -PI³ u ³)
| f '(u) | = PI u
| f '(u) × f ''(u) | = PI³ u ³
k (u) = 1

g '(v) = (PI v cos(v ² PI/2), -PI v sin(v ² PI/2), 0)
g ''(v) = (-PI² v ² cos(v ² PI/2), -PI² v ² cos(v ² PI/2), 0)
g '(v) × g ''(v) = (0, 0, -PI³ u ³)
| g '(v) | = PI v
| g '(v) × g ''(v) | = PI³ v ³
k (v) = 1

Заметьте, что и g '(0), и g ''(0) - вектора нулевой длины, и поэтому неопределены. В итоге мы вообще не можем ничего сказать о непрерывности; но по рисунку "кажется", что они непрерывны, хотя бы потому, что у них общая касательная в точке соединения.

Как вы уже, наверное, догадались, щас будем опять все это дело перепараметризовывать. (Жуткое слово, согласен. - прим. перев.) Заменим u ² на p в f (u) и v ² на q в g (v). Получим такие уравнения:

f (p) = (-cos(p PI/2), sin(p PI/2), 0)
g (q) = (sin(q PI/2), cos(q PI/2), 0)

Их производные:

f '(p) = ((PI/2) sin(p PI/2), (PI/2) cos(p PI/2), 0)
f ''(p) = ((PI/2)² cos(p PI/2), -(PI/2)² sin(p PI/2), 0)

g '(q) = ((PI/2) cos(q PI/2), -(PI/2) sin(q PI/2), 0)
g ''(q) = (-(PI/2)² sin(q PI/2), -(PI/2)² cos(q PI/2), 0)

f '(p) × f ''(p) = g '(q) × g ''(q) = (0, 0, -(PI/2)³)
| f '(p) × f ''(p) | = | g '(q) × g ''(q) | = (PI/2)³
| f '(p) | = | g '(q) | = PI/2
k (p) = k (q) = 1

Следовательно, после замены переменных и f '(1) и g '(0) равны (PI/2, 0, 0) и поэтому они являются C ¹ непрерывными. Более того, и f ''(1) и g ''(0) равны (0, -(PI/2)², 0), и поэтому они C ² непрерывны! Они также непрерывны по кривизне, так как их кривизна везде равна 1 (это окружности). Вот она какая, эта перепараметризация. 8)

Дата добавления: 2015-10-29