Нормальный Вектор и Кривизна

Возьмем фиксированную точку f (u) и две движущихся P и Q на параметрической кривой. Три эти точки единственно определяют плоскость. По мере того, как P и Q движутся к f (u), эта плоскость приближается к какому-то определенному положению. Это касательная плоскость к f (u). Конечно, кас. плоскость к f (u) содержит и касательную прямую к этой кривой. Можно показать, что кас. плоскость - плоскость, проходящая через f (u) и содержащая как f '(u), так и f ''(u). Говоря точнее, любая точка на этой плоскости имеет следующее уравнение, где p и q - параметры:

f (u) + p f '(u) + q f ''(u)

Бинормальный вектор b (u) - это единичный вектор векторного произведения f '(u) и f ''(u):

b (u) = (f '(u) × f ''(u)) / | (f '(u) × f ''(u)) |

То есть, бинормальный вектор b (u) перпендикулярен как f '(u), так и f ''(u), а значит, и касательной плоскости. Прямая f (u)+ t b (u) - это бинормальная прямая к f (u).

Нормальный вектор - перпендикулярен касательному и бинормальному векторам, и направлен по правилу правой руки. То есть, единичный нормальный вектор n (u) определяется как

n (u) = (b (u) × f '(u)) / | b (u) × f '(u) |

Прямая f (u)+ t n (u) - это нормальная прямая к f (u). Таким образом, касательный вектор f '(u), нормальный вектор n (u) и бинормальный вектор b (u) образуют коорд. систему с началом координат в f (u). Касательная прямая, бинормальная прямая и нормальная прямая - это коорд. оси этой системы с положительными направлениями соответственно по направлениям касательного, бинормального и нормального векторов. Три эти вектора обычно называют направляющей триадой (тройкой?) [??? moving triad] или просто триадой в точке f (u). Направл. тройку также называют направляющим трехгранником. Вот рисунок, поясняющий их взаимное расположение. Заметьте, что касательный вектор, нормальный вектор и вектор f ''(u) лежат на одной плоскости.

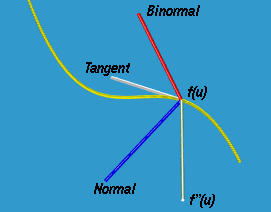
(Tangent - касательный.)

Пример

Вычмслим касательный, бинормальный и нормальный вектора для круговой спирали:

f (u) = (a cos(u), a sin(u), bu)

Первая и вторая производные:

f '(u) = (- a sin(u), a cos(u), b)
f ''(u) = (- a cos(u), - a sin(u), 0)

Не-единичный бинормальный вектор - это векторное произведение f '(u) и f ''(u), то есть:

b (u) = f '(u) × f ''(u) = (ab sin(u), - ab cos(u), a ²)

Не-единичный нормальный вектор - это векторное произведение бинормального и касательного векторов, то есть:

n (u) = b (u) × f '(u) = (- a (a ² + b ²)cos(u), - a (a ² + b ²)sin(u), 0)

Сравнив n (u) и f ''(u), видим, что они параллельны друг другу (т.e. их коэффициенты пропорциональны). В итоге, после нормализации всех участвующих векторов, векторы нормали и второй производной равны. Это показано на следующем рисунке. Вычисления для u = 1.

Кривизна

Тут объясняется про кривизну.

Значение кривизны, k (u), можно найти так:

k (u) = | f '(u) × f ''(u) | / | f '(u) |³

Возьмем круговую спираль из предыдущего примера. Из вычислений f '(u) и f ''(u), имеем

f '(u) = (- a sin(u), a cos(u), b)
f '(u) × f ''(u) = (ab sin(u), - ab cos(u), a ²)
| f '(u) | = SQRT (a ² + b ²)
| f '(u) × f ''(u) | = a SQRT (a ² + b ²)
k (u) = a / (a ² + b ²)

Отсюда, кривизна спирали в каждой точке постоянна и равна a /(a ² + b²).

Так как радиус окружности кривизны равен 1/ k, получается, что центр этой окружности расположен на расстоянии (a ² + b ²)/ a от f (u) в направлении n (u).

Еще примеры

• Дана прямая:

f (u) = (a + up, b + uq, c + ur)

Имеем:

f '(u) = (p, q, r)
| f '(u) | = SQRT (p ² + q ² + r ²)
f ''(u) = (0, 0, 0)
f '(u) × f ''(u) = (0, 0, 0)
k (u) = 0

То есть, в любой точке прямой ее кривизна равна 0.

• Дана окружность на плоскости xy:

f (u) = (r cos(u) + p, r sin(u) + q, 0)

Так как она на плоскости xy, третья координата всегда 0. Имеем:

f '(u) = (- r sin(u), r cos(u), 0)
f ''(u) = (- r cos(u), - r sin(u), 0)
f '(u) × f ''(u) = (0, 0, r ²)
| f '(u) | = r
| f '(u) × f ''(u) | = r ²
b (u) = (f '(u) × f ''(u)) / | f '(u) × f ''(u) | = (0, 0, 1)
n (u) = (b (u) × f '(u)) / | b (u) × f '(u) | = (-cos(u), -sin(u), 0)
k (u) = 1/ r

Таким образом, касательный вектор равен (-sin(u), cos(u), 0), бинормальный (0, 0, 1), а нормальный (-cos(u), sin(u), 0). Кривизна окружности постоянна и равна 1/ r. Получаем, что радиус окружности кривизны равен r и окружность сама является окружностью кривизны.

• Дана кубическая кривая [space cubic] в пространстве:

f (u) = (u, u ², u ³)

Вычисление кривизны: k (u):

f '(u) = (1, 2 u, 3 u ²)
| f '(u) | = SQRT (1 + 4 u + 9 u ⁴)
f ''(u) = (0, 2, 6 u)
f '(u) × f ''(u) = (6 u ², -6 u, 2)
| f '(u) × f ''(u) | = 2 SQRT (1 + 9 u ² + 9 u ⁴)
k (u) = 2 SQRT (1 + 9 u ² + 9 u ⁴) / (SQRT (1 + 4 u ² + 9 u ⁴))³

Дата добавления: 2015-10-29