Рациональные Формы Стандартных Кривых

Найдем рациональную форму окружности.

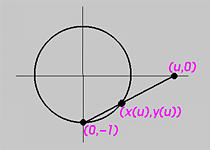
На рисунке - окружность с центром в начале координат и радиусом 1. Пусть u будет параметром для этой окружнотси. Для общей пользы будем использовать ось x для значений u, то есть каждому отдельному значению u соответствует точка (u,0) на оси x. Проведем прямую от (u,0) до низа окружности, (0,-1). Так как прямая пересекает окружность в двух точках, пусть другая точка, не низ окружности, будет (x (u), y (u)). По мере того, как u перемещается по оси x, соответствующая ей точка движется по окружности. Для любого конечного u есть соответствующая точка. Бесконечному значению u соответствует низ окружности. С другой стороны, любая точка на окружности, не являющаяся самой нижней, соотвтетствует значению u на оси x.

Прямая, соединяющая нижнюю точку окружности и (u,0) - x = uy + u. Уравнение окружности - x ² + y ² = 1. Подставляя уравнение прямой в уравнение окружности и решая его относительно y, получим два корня. Один из них должен быть y = -1, так как эта прямая проходит через нижнюю точку окружности. Другой корень y = (1 - u ²) / (1 + u ²). Подставляя это значение y в уравнение прямой, получаем x = (2 u) / (1 + u ²). Таким образом, для каждого значения u, соответствующая точка на окружности имеет координаты

x = 2 u / (1 + u ²)
y = (1 - u ²) / (1 + u ²)

В итоге, окружность имеет рациональную параметризацию. Когда u стремится к бесконечности, x достигает 0, тогда как y достигает -1.

Фактически, это вычисление дает нам еще кое-что. Эта окружность имеет тригонометрическую параметрическую форму (cos(t), sin(t)), где t в пределах от 0 до 2PI. Таким образом, точка на окружности может иметь два различных представления, значения которых одинаковы. То есть, (cos(t), sin(t)) = ((2 u) / (1 + u ²), (1 - u ²) / (1 + u ²)) для некоторого u. Таким образом, тригоном. функции cos(t) и sin(t) могут быть параметризованы следующим образом:

cos(t) = 2 u / (1 + u ²)
sin(t) = (1 - u ²) / (1 + u ²)

Используя параметризацию для cos(t) и sin(t), можно легко найти рациональную параметризацию для эллипса и гиперболы. Гиперболу рассмотрим сейчас, а эллипс оставим как упражнение. Гипербола в нормальной форме имеет уравнение след. вида:

x ²/ a ² - y ²/ b ² = 1,

где a и b - это длины главной и второстепенной полуосей. Легко проверить, что это правильная параметризация для гиперболы:

x = a sec(t)
y = b tg(t)

Так как tg(t) = sin(t) / cos(t), а sec(t) = 1 / cos(t), подставив рациональную параметризацию для sin(t) и cos(t) в эти уравнения, преобразовываем их от тригонометрической параметрической формы в рациональную:

x = a (1 + u ²) / (2 u)
y = b (1 - u ²) / (2 u)

Теоремы Объединения [Uniformization]

Вы видели способ преобразования многочлена в параметрической форме в многочлен p (x, y) = 0 в предыдущем примере. Рациональные формы также можно преобразовывать в многочлены. Загвоздка в устранении параметра u из всех параметрических уравнений. Это сложно, но, как говорится, можно. Фактически, с помощью теории исключения, можно преобразовать полиномиальную или рациональную параметрическую форму в многочлен с двумя переменными. Это называется приведением к явному виду [implicitization].

Вопрос: если кривая задана в форме многочлена явно, можно ли найти параметрическую форму, полиномиальную или рациональную, чтобы она описывала ту же самую кривую? К сожалению, нет. То есть, существуют кривые, не имеющие параметрического рационального представления или в виде многочлена (напр., эллиптическая кривая y ² = x ³ + ax + c). Это результат теорем объединения.

По этой причине с помощью явных многочленов можно описать больше разных кривых, чем с помощью полиномиальной и рациональной параметрической форм. Почему бы не использовать явные многочлены направо и налево? Дело вот в чем. Параметрические кривые использовать легко. И хоть явные многочлены являются мощным средством, с помощью которого можно описать разные кривые, многие их важные свойства трудно рассчитывать и, вообще, явные многочлены - это тяжело. Поговорим об этом позже.

Спрашивается: зачем нам нужны новые виды параметрических кривых? Наверное, ответ в том, что те кривые, что мы рассматривали в прошлых темах, не очень-то и геометрические. Точнее говоря, по алгебраической записи не скажешь, как будет выглядеть кривая, пока не проанализируешь ее. Коэффициенты не имеют геометрического значения, так что непонятно, как изменится форма кривой, если изменить какие-то коэффициенты. И в итоге разработать вид кривой так, чтобы ее форма соответствовала запросам, очень сложно.

На практике проектировщикам и пользователям вообще фиолетово, что там за математика (и уравнения) у этой кривой. Их больше заботит, сделана ли их работа. Поэтому система, предоставляющая пользователям возможность проектирования кривых должна быть

1. Интуитивной:
   В общем, понятной для обезьян и студентов.
2. Гибкой:
   Чтобы можно было выполнять больше разных операций над объектами.
3. Единые Методы:
   То есть, принципы создания и редактирования разных объектов должны быть едиными.
4. Инвариантность:
   Кривая не должна изменять своей геометрии при таких преобразованиях, как перенос, поворот и проецирование.
5. Эффективность и Численная Устойчивость: Пользователю системы разработки кривых может быть пофигу, что там за геометрия; ему надо, чтобы система выдала нужную ему кривую быстро и точно. А также, большое количество вычислений не должно "исказить" форму кривой (это и есть численная устойчивость).

В этом разделе мы обсудим некоторые техники разработки кривых, соответствующие вышеизложенным критериям. Обсудим кривые Безье, рациональные кривые Безье, кривые B-spline и NURBS. Тема дает следующие возможности:

1. Пользователь задает набор контрольных точек для системы, чтобы для начала получить кривую, хотя бы более или менее следующей по направлению этого набора точек.
2. Пользователь может изменять положения некоторых контрольных точек и некоторые другие параметры, чтобы изменить вид кривой.
3. Если необходимо, пользователь может добавлять какую-то информацию без изменения формы кривой. Таким образом, он получает больше возможностей, так как добавление контрольных точек и другой информации увеличивает количество степеней свободы кривой.
4. Пользователь также может разрывать кривую на две части для более тщательного редактирования, а затем снова соединять их вместе.
5. Есть геометрические, интуитивные и численно стойкие алгоритмы для нахождения точек на кривой без знания ее уравнения.
6. Зная кривые, перейти к поверхностям будет несложно.

И кривые Безье, и B-spline - полиномиальные параметрические кривые Как уже обсуждалось, такие кривые не могут быть использованы для представления некоторых простых кривых, например, окружностей. При введении [homogeneous] координат, делающих их рациональными, кривые Безье и B-spline обобщаются до рациональных кривых Безье и неравномерных рациональных B-сплайнов (N on- U niform R ational B -splines), сокращенно NURBS. Очевидно, что рациональные кривые Безье более сильные, чем просто кривые Безье, так как с помощью рациональных можно также представлять и окружности и эллипсы. Аналогично, NURBS сильнее B-сплайнов. Вот соотношение между этими четырьмя типами представления кривых.

Дата добавления: 2015-10-29