Построение Кривых Безье

Дано n +1 точек p ₀, p ₁, p ₂,... и p _n в пространстве - контрольные точки. Кривая Безье, описываемая этими точками -

,

где коэффициенты, коэффициенты Безье, равны:

Таким образом, точка, соответствующая u на кривой Безье - это "среднее взвешенное" между всеми точками, где вес каждой точки - это коэффициент B_{n , i} (u). Отрезки p ₀ p ₁, p ₁ p ₂,..., p _{n -1} p _n, называются сегментами ["legs" - ноги 8-) ], они образуют контрольную ломаную. Некоторые авторы называют эту ломаную контрольным многоугольником. Функции B_{n , i} (u), 0 <= i <= n, обычно называют функциями базиса[basis] Безье.

Заметьте, что u в пределах [0,1]. Поэтому все коэффициенты неотрицательны. Далее, так как и u, и i могут равняться 0, как и 1 - u и n - i, примем неопределенность 0⁰ равной 1. Далее показана кривая Безье, построенная по 11 контрольным точкам, для синей точки на кривой u =0.4. Как видно с рисунка, кривая более или менее следует за ломаной.

Важны следующие свойства кривых Безье:

1. Степень кривой Безье, посторенной по n +1 контрольным точкам, равна n:
   В каждом коэффициенте, показатель степени u равен i + (n - i) = n. Таким образом, степень кривой равна n.
2. p(u) проходит через p₀ и p _n:
   Это изображено на рисунке выше. Кривая, показана красным, проходит через первую и последнюю контрольные точки.
3. Неотрицательность:
   Все коэффициенты кривых Безье неотрицательны, как уже говорилось раньше.
4. Деление Единства [Partition of Unity]:
   Количество коэффициентов Безье равно n + 1. Более того, их сумма равна 1. Все коэффициенты Безье - коэффициенты в разложении выражения 1 = (u + (1 - u)) ⁿ. Отсюда, их сумма равна 1. А так как они неотрицательны, получаем, что каждый из них находится в пределах от 0 до 1.

На рисунке слева кривая Безье, построенная по пяти контрольным точкам. Ее коэффициенты Безье - это функции от u, показаны на рисунке справа. Рисунок показывает u =0.5 и пять коэффициентов Безье. А вертикальная линия показывает деление 1 на пять интервалов, отсюда название деление единства. Заметьте, цвета в делении те же, что и у коэффициентов Безье.

Так как все коэффициенты Безье в пределах от 0 до 1, каждый из них можно представить как вес при вычислении среднего взвешенного. Точнее, можно сказать "чтобы вычислить p (u), берем вес B_n,i (u) для контрольной точки p _i и суммируем их все."

1. Свойство Ограничивающего Многоугольника:
   Это значит, что кривая Безье, постороенная по данным n + 1 точкам, лежит польностью внутри ограничивающего многоугольника данных точек. Ограничивающий многоугольник для набора точек - это наименьший многоугольник, содержащий все эти точки. Отрезок, соединяющий две соседние точки в огр. многоугольнике, также содержится в нем. На рисунке ограничивающий многоугольник показан серым цветом. Заметьте, не все контрольные точки лежат на сторонах огр. многоугольника. Например, контрольные точки 3, 4, 5, 6, 8 и 9 находятся внутри него. Кривая, за исключением крайних точек, находится полностью внутри огр. многоугольника.

Это свойство важно, потому что мы гарантированно знаем, что полученная кривая будет в понятной и вычисляемой области и не выйдет за ее пределы. В какой-то мере, построенная кривая очень предсказуема.

1. Свойство Уменьшения Изменчивости:
   Если кривая лежит на плоскости, это значит, что нет такой прямой, которая пересекала бы кривую Безье больше раз, чем ее контрольную ломаную.

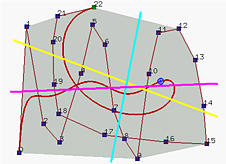
Взгляните на рисунок. Желтая линия пересекает кривую 3 раза, а ломаную 7 раз; фиолетовая линия пересекает кривую 5 раз, ломаную 7 раз; голубая линия пересекает и кривую, и ломаную дважды.

Если кривая пространственная, достаточно заменить "прямую" на "плоскость". Есть особые случаи; тем не менее, несложно придумать такую схему подсчета, чтобы она подходила для всех случаев.

Так что же это за свойство такое и причем тут изменчивость? Это свойство говорит о том, что сложность (т.е. повороты и изгибы) кривой не сложнее, чем у ее контрольной ломаной. Взгляните на рисунок выше - ломаная запутаннее кривой, построенной по ней.

Дата добавления: 2015-10-29