Введение Узла для Кривых NURBS

Только что обсуждалось введение узла для кривых B-spline. Так как кривые NURBS - это проекции 4D-кривых B-spline на 3D-пространство, то введение узлов для кривых NURBS - это довольно просто. Заметьте, вышеизложенное обсуждение и вычисления не требуют, чтобы контр. точки были в трехмерном пространстве. Таким образом, введение узла для кривых NURBS делается в три шага: (1) преобразуем данную кривую NURBS в 3D в кривую B-spline в 4D, (2) проводим введение узла для этой четырехмерной кривой B-spline, и (3) проецируем новый набор контр. точек обратно на трехмерное пространство, чтобы получить новый набор контр. точек для данной кривой NURBS после введения узла.

Пусть имеется n + 1 контр. точек p ₀, p ₁,..., p _n с соответствующими весами w ₀, w ₁,..., w_n, узловой вектор U и степень p. Пусть p _i = (x_i, y_i, z_i). Тогда контр. точки P _i = (w_ix_i, w_iy_i, w_iz_i, w_i), 0 <= i <= n и узловой вектор U определяют четырехмерную кривую B-spline степени p. Мы можем ввести узел t в эту четырехмерную кривую B-spline, получим новый набор контр. точек Q _i = (X_i, Y_i, Z_i, W_i), 0 <= i <= n. Проецируем эти контр. точки обратно на трехмерное пространство с помощью деления первых трех составляющих на четвертую, и получаем новый набор контр. точек для данной кривой NURBS.

Рассмотрим пример. Допустим, есть 9 узлов

u 0 - u 3	u 4	u 5 - u 8
	0.5

и кривая NURBS 3 степени, построенная по 5 контр. точкам на плоскости xy:

	x	y	w
p0	-70	-76
p1	-70		0.5
p2
p3		-77
p4	-40	-76

Вот кривая и ее базисные функции.

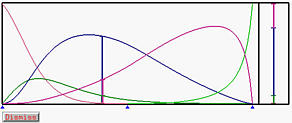
Давайте введем новый узел t = 0.4. Так как t на узловом интервале [ u ₃, u ₄), а степень кривой NURBS равна 3, то зависимые точки - это p ₃, p ₂, p ₁ и p ₀. Так как это кривая NURBS, мы будем использовать [homogeneous] кординаты, умножив все контр. точки на соответствующие им весы. Назовем эти новые точки P _i:

	x	y	w
P0	-70	-76
P1	-35	37.5	0.5
P2
P3		-385

Заметьте, так как на P ₄ не влияет введение узла, она не вычисляется в этой таблице. Затем, вычисляем a ₃, a ₂ и a ₁:

a ₃ = (t - u ₃)/ (u ₆ - u ₃) = (0.4 - 0)/(1 - 0) = 0.4
a ₂ = (t - u ₂)/ (u ₅ - u ₂) = (0.4 - 0)/(1 - 0) = 0.4
a ₁ = (t - u ₁)/ (u ₄ - u ₁) = (0.4 - 0)/(0.5 - 0) = 0.8

Новые контр. точки Q ₃, Q ₂ и Q ₁ - это

Q ₃ = (1 - a ₃) P ₂ + a ₃ P ₃ = (325.6, 26, 4.4)
Q ₂ = (1 - a ₂) P ₁ + a ₂ P ₂ = (97.4, 142.5, 1.9)
Q ₁ = (1 - a ₁) P ₀ + a ₁ P ₁ = (-42, 14.8, 0.6)

Проецируя эти три четырехмерные контр. точки с помощью деления первых трех составляющих на четвертую (вес), получим

q ₃ = (74, 5.9) с весом 4.4
q ₂ = (51.3, 75) с весом 1.9
q ₁ = (-70, 24.6) с весом 0.6

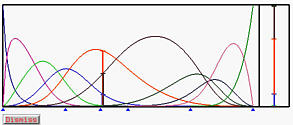
Вот конечный вид кривой NURBS и ее базисных функций:

Дата добавления: 2015-10-29