Замечание [Наблюдение] II: Вычисление Новых Контрольных Точек

Вспомним из способа введения узла в существующий узел, что, если t вводится в существующий узел u_k множественности s, то контр. точки p _k-s, p _{k-s +1},..., p _{k -1} и p _k не влияют, и только p _k-p, p _{k-p +1},..., p _k-s участвуют в вычислении новых контр. точек q _i. Перепишем все новые контр. точки после первого введения со вторым нижним индексом 1. Таким образом, имеем следующую диаграмму:

Если один и тот же узел вводится второй раз, то зависящие [affected] p +1 контр. точек - это p _k, p _{k -1}, p _k-s, p _{k-s ,1}, p _{k-s -1,1},..., p _{k-p +1,1}, как показано в вышеукзанной диаграмме. Заметьте, что p _k-p исключается, так как только p +1 контр. точек зависимы [affected]. Тем не менее, так как множественность t увеличивается на единицу из-за первого введения, то s +2 контр. точек не будут участвовать вычислении введения узла: p _k, p _{k -1},..., p _k-s и p _{k-s ,1}. Схема вычисления и новый набор точек показаны ниже. Заметьте, что новые контр. точки, полученные после второго введения узла, имеют в качестве второго нижнего индекса число 2. Новые контр. точки - это: (1) p _{k-p +1,1} и p _{k-s ,1}, полученные после первого введения узла, и (2) p _{k-p +2,2} - p _{k-s ,2}, полученные после второго введения узла.

Для третьего введения, зависимые p +1 контр. точек - это от p _{k-p +2,2} до p _{k-s ,2}, p _{k-s ,1}, и от p _k-s до p _k. Так как третье введение вновь увеличивает множественность t на единицу, то количество контр. точек, которое не участвует в вычислении, также увеличивается на единицу. В итоге, p _{k-s ,2} останется неизменным как до третьего введения, так и после него. Это показывает следующая диаграмма:

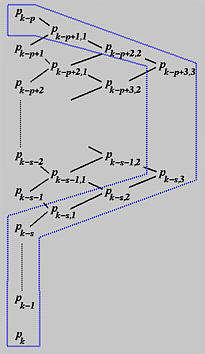
В общем случае, если t вводится h раз в узлы u_k множественности s, где s = 0 означает, что t вводится в середине этого узлового интервала, а s > 0 значит, что t вводится в множественный узел, то можно:

1. записать первый набор p +1 зависимых контр. точек в качестве нулевого столбца;
2. пропустить последние s контр. точек (т.e. от p _{k-s +1} до p _k);
3. вычислить первый столбец, второй столбец,... и h -ый столбец;
4. новым набором контр. точек будут те, что ограничены пунктирным многоугольником.

Итоги

Объединяя эти два наблюдения, полусим следующий алгоритм для введения узла t несколько раз.

Входные данные: узел t на [ u_k, u_{k +1}) с исходной множественностью s, который нужно ввести h раз, где h+s меньше или равно p, степень данной кривой B-spline или NURBS
Выходные данные: новый набор контр. точек после того, как t введен h раз

Переименуем контр. точки p _k, p _{k -1},..., p _k-p как p _{k ,0}, p _{k -1,0},..., p _{k-p ,0}, т.е. добавим второй нижний индекс 0.

for r:= 1 to h do

for i:= k-p+r to k-s do

Begin

Let a_i,r = (t - u_i) / (u_{i+p-r +1} - u_i)
Пусть p _i,r = (1 - a_i,r) p _{i -1, r -1} + a_i,r p _{i , r -1}

End

Новый набор контр. точек образуется из исходных от p ₀ до p _k-p, следуя по верхнему краю вышеизложенной диаграммы (т.e. p _{k-p +1,1}, p _{k-p +2,2},..., p _k-p+h,h), потом по правому краю диаграммы (т.e. p _{k-p+h +1, h} , p _{k-p+h +2, h} ,...., p _{k-s , h} ), потом по низу диаграммы (т.e. p _{k-s , h -1}, p _{k-s , h -2},...., p _{k-s ,1}), потом по исходным контр. точкам p _k-s,..., p _k,..., p _n.

Дата добавления: 2015-10-29