NURBS: Определение

Давайте рассмотрим способ введения [homogeneous] координат в кривые B-spline и найдем определение NURBS.

Дано n +1 контр. точек p ₀, p ₁,..., p _n и узловой вектор U = { u ₀, u ₁,..., u_m } из m +1 узлов, кривая B-spline степени p описывается этими параметрами так:

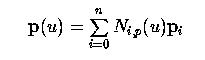
Перепишем контр. точку p _i в виде вектора-столбца с четырьмя составляющими, четвертая из которых равна 1:

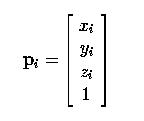
Для [homogeneous] координат, умножение координат точки на не равное нулю число не изменяет ее положения. Умножим координаты p _i на w_i, чтобы получить новую форму [homogeneous] координат:

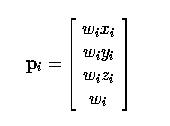
Подставляя эту новую [homogeneous] форму в вышеуказанное уравнение кривой B-spline, получим следующее:

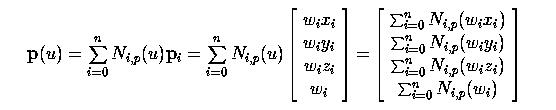
Таким образом, точка p (u) получается также в [homogeneous] координатной форме. Преобразуем ее обратно в Декартовы координаты делением p (u) на четвертую кординату:

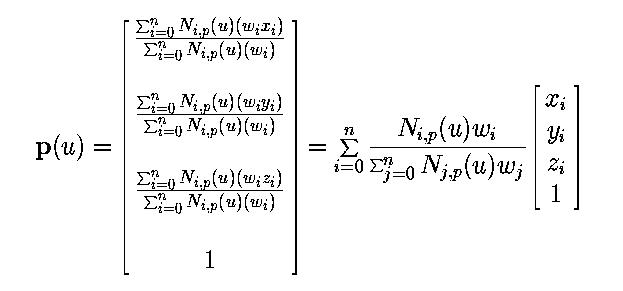
В итоге получим такой понятный вид:

Это кривая NURBS степени p, описываемая контр. точками p ₀, p ₁,..., p _n, узловым вектором U = { u ₀, u ₁,..., u_m }, и весами w ₀, w ₁,.., w_n. Заметьте, что так как вес w_i связан с четвертой составляющей соотв. контр. точки p _i, то количество весов и количество контр. точек должны быть одинаковыми.

В общем случае, весы wi положительны; но отрицательные весы имеют интересные приложения. Если вес, скажем, wi, становится равным нулю, то коэффициент при pi равен нулю и, следовательно, контр. точка pi не влияет на вычисление p(u) для любого u (т.e. pi "выключена"). Кроме того, нулевые весы также имеют полезные интерпретации, называемые бесконечными контр. точками. Мы обсудим это понятие позже.

Два Прмых Следствия [Two Immediate Results]

Вот два результата, следующих прямо из определения.

1. Если все весы равны 1, кривая NURBS вырождается в B-spline.
   Это очевидно, так как в этом случае точки в [homogeneous] координатах идентичны их Декартовой форме и знаменатель равен 1.
2. Кривые NURBS - Рациональные
   Это также очевидно. Значение, умноженное на контрольную точку p _i, N_i,p (u) w_i, - это многочлен степени p. Знаменатель - это сумма всех коэффициентов, и поэтому также является многочленом степени p. В итоге, коээфициент контр. точки p _i равен частному двух многочленов степени p и функция p (u) - рациональная.

Два этих результата указывают на то, что кривые B-spline - это частный случай кривых NURBS. Более того, так как кривые NURBS - рациональные, то окружности, эллипсы и многие другие кривые можно представить с помощью кривых NURBS.

Дата добавления: 2015-10-29