Кривые B-spline: Важные Свойства

У кривых B-spline много свойств, схожих с кривыми Безье, так как они являются обощением последних. Более того, кривые B-spline имеют больше желаемых свойств, чем кривые Безье. На этой странице перечислено большинство важных свойств B-spline. Мы рассмотрим только фиксированные кривые B-spline.

В дальнейшем будем считать, что кривая B-spline p (u) степени p определяется n + 1 контрольными точками, узловым вектором U = { u ₀, u ₁,...., u_m } с первыми p +1 и последними p +1 "склеенными" узлами (т.e. u ₀ = u ₁ =... = u_p и u_m-p = u_{m-p +1} =... = u_m).

1. Кривая B-spline p(u) является кусочной кривой, каждый компонент которой - кривая степени p.
   Как упоминалось на предыдущей странице, p (u) можно представить как объединение отрезков кривых, построенных на каждом узловом интервале. На рисунке ниже, при n = 10, m = 14 и p = 3, четыре первых и четыре последних узла фиксированы, а 7 средних узлов равномерно распределены. Всего 8 узловых интервалов, каждый из которых соответствует отрезку кривой. Делящие точки - это p (u_i). На рисунке слева эти точки показаны треугольниками.

Это полезное свойство дает нам возможность проектировать кривые очень сложных форм, используя многочлены низких степеней. Например, ниже правый рисунок показывает кривую Безье с тем же набором контрольных точек. Кривая не очень-то следует за контрольной ломаной, а ее степень равна 10!

В общем случае, чем меньше степень, тем сильнее кривая B-spline приближается к ее контрольной ломаной. На рисунках далее показаны кривые с одной и той же контрольной ломаной, их узлы фиксированы и равномерно распределены. На первом рисунке кривая 7 степени, на среднем - 5, а на правом - 3. Таким образом, при увеличении степени полученный B-spline приближается к его контрольной ломаной.

1. Равенство m = n + p + 1 должно выполняться
   Так как для каждой контрольной точки нужна базисная функция и количество базисных функций удовлетворяет условию m = n + p + 1.
2. Фиксированный кривая B-spline p(u) проходит через две крайние контр. точки p₀ и p _n
   Заметьте, что базисная функция N _{0, p} (u) - это коэффициент контрольной точки p ₀ и не равна нулю на [ u ₀, u_{p +1}). Так как u ₀ = u ₁ =... = u_p = 0 для фиксированной кривой B-spline, N _0,0(u), N _1,0(u),...., N_{p -1,0}(u) равны нулю и только N_{p ,0}(u) не равно нулю (вспомните из треугольной формы расчета). Следовательно, когда u = 0, N _{0, p} (0) равно 1 и p (0) = p ₀. Аналогичные рассуждения могут показать, что p (1) = p _n
3. Свойство Сильного Ограничивающего Многоугольника [Strong Convex Hull Property]: кривая B-spline содержится в ограничивающем многоугольнике ее контрольной ломаной. Говоря точнее, если u лежит на узловом интервале [ u_i, u_{i +1}), то p(u) находится в ограничивающем многоугольнике контр. точек p _i-p, p _{i-p +1},..., p _i
   Если u лежит на узловом интервале [ u_i, u_{i +1}), есть только p +1 базисных функций (i.e., N_{i , p} (u),..., N_{i-p +1, p} (u), N_{i-p , p} (u)), ненулевых на этом узловом интервале. Так как N_k,p (u) - это коэффициент контр. точки p _k, только p +1 контр. точек p _i, p _{i -1}, p _{i -2},.., p _i-p имеют ненулевые коэффициенты. Так как на этом узловом интервале базисные функции не равны нулю и в сумме составляют 1, их точка "среднего взвешенного", p (u), должна находится внутри ограничивающего многоугольника контр. точек p _i, p _{i -1}, p _{i -2},.., p _i-p. Значение слова "сильный" в том, что кроме того, что p (u) лежит внутри ограничивающего многоугольника всех точек, она находится еще и внутри гораздо меньшего многоугольника.

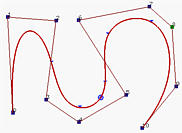
Две показаные выше кривые B-spline имеют 11 контр. точек (т.e. n = 10), 3 степени (т.e. p =3) и 15 узлов (m = 14), четыре первых и четыре последних узла фиксированы. Таким образом, количество узловых интервалов равно количеству отрезков кривых. Узловой вектор - это

u 0

u 1

u 2

u 3

u 4

u 5

u 6

u 7

u 8

u 9

u 10

u 11

u 12

u 13

u 14

0.12

0.25

0.37

0.5

0.62

0.75

0.87

На рисунке слева u лежит на узловом интервале [ u ₄, u ₅) = [0.12,0.25), а соответствующая точка (т.e. p (u)) - на втором отрезке кривой. Таким образом, p +1 = 4 базисных функции - ненулевые на этом интервале (т.e. N _4,3(u), N _3,3(u), N _2,3(u) и N _1,3(u)), а соответствующие контрольные точки - это p ₄, p ₃, p ₂ и p ₁. Темная область - это огранич. многоугольник для этих четырех точек. Ясно, что p (u) лежит в этом многоугольнике.

Кривая B-spline на правом рисунке описывается так же. Но в данном случае u на интервале [ u ₉, u ₁₀) = [0.75,0.87) и ненулевые функции - это N _9,3(u), N _8,3(u), N _7,3(u) и N _6,3(u). Соответствующие контрольные точки - p ₉, p ₈, p ₇ и p ₆.

Следовательно, когда u движется от 0 к 1 и переходит узел, базисные функции становятся нулями, а новая базисная функция становится эффективной. В результате одна контрольная точка, коэффициент которой становится равным 0, выходит за пределы огранич. многоугольника и заменяется новой контрольной точкой, коэффициент которой не равен нулю.

1. Схема Локального Изменения [Local Modification Scheme]: имзенение положения контрольной точки p _i влияет только на кривую p(u) на интервале [ u_i, u_{i+p +1})
   Это следует из другого важного свойства базисных функций B-spline. Вспомним, что N_i,p (u) не равно нулю на интервале [ u_i, u_{i+p +1}). Если u не на этом интервале, то N_i,p (u) p _i не влияет на вычисление p (u), так как N_i,p (u) равно нулю. С другой стороны, если u находится в указанном интервале, N_i,p (u) не равно нулю. Если p _i изменяет положение, N_i,p (u) p _i тоже изменяется и, следовательно, изменяется и p (u).

Вышеуказанные кривые B-spline имеют те же параметры, что и в предыдущем примере. Переместим контр. точку p ₂. Коэффициент этой контр. точки равен N _2,3(u), а интервал, на котором этот коэффициент не равен нулю - это [ u ₂, u ₂₊₃₊₁) = [ u ₂, u ₆) = [0,0.37). Так как u ₂ = u ₃ = 0, то только три отрезка, соответствующих [ u ₃, u ₄) (область первого отрезка кривой), [ u ₄, u ₅) (область второго отрезка кривой) и [ u ₅, u ₆) (область третьего отрезка кривой) будут затронуты. Рисунок справа показывает результат перемещения p ₂ в правый нижний угол. Как видите, только первый, второй и третий отрезки кривой изменили форму, а все остальные остались неизменными.

Эта схема локального изменения очень важна для проектирования кривых, потому что можно изменять кривую локально, не изменяя форму кривой в целом. Более того, если нужна точная настройка кривой, можно добавить больше узлов (соответственно, и контр. точек) так, чтобы зона изменения была очень малой областью. Мы поговорим об добавлении узлов позже.

1. p(u) имеет непрерывность C^p-k в узле множественности k
   Если u - это не узел, то p (u) находится в середине отрезка кривой степени p, и поэтому бесконечно дифференцируема. Если u - это узел на ненулевой области определения N_i,p (u), так как последняя только C^p-k -непрерывна, то и p (u) тоже.

Вышеуказанная кривая имеет 18 контр. точек (т.e. n = 17), степень, равную 4, и следующий фиксированный узловой вектор

от u 0 до u 4	u 5	u 6 и u 7	u 8	от u 9 до u 11	u 12	от u 13 до u 16	u 17	от u 18 до u 22
	0.125	0.25	0.375	0.5	0.625	0.75	0.875

Таким образом, u ₆ является двойным узлом, u ₉ тройным узлом, а u ₁₃ - четверным. Следовательно, p (u) имеет непрерывность C ⁴ в любой точке, не являющейся узлом, непрерывность C ³ во всех простых узлах, непрерывность C ² в u ₆, непрерывность C ¹ в u ₉, непрерывность C ⁰ в u ₁₃.

Все точки на кривой, соответствующие узлам, обозначены маленькими треугольниками, соответствующие множественным узлам - окружностями с числом, указывающим их множественность. Очень сложно зрительно показать разницу между непрерывностями C ⁴, C ³ и даже C ². Для случая C ¹ соответствующая точка лежит на сегменте, тогда как в случае C ⁰ кривая проходит через контрольную точку. Мы еще вернемся к этому позднее, при обсуждении изменения узлов.

1. Свойство Уменьшения Изменчивости [Variation Diminishing Property]:
   Свойство уменьшения изменчивости также подходит и для кривых B-spline. Если кривая на плоскости (соотв., в пространстве), это значит, что не существует прямой (соотв., плоскости), пересекающей кривую B-spline больше раз, чем ее контрольную ломаную.

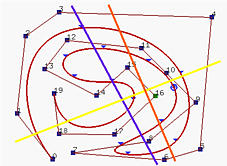
На рисунке выше синяя линия пересекает как контрольную ломаную, так и кривую B-spline 6 раз, тогда как желтая линия пересекает их по 5 раз. Однако оранжевая линия пересекает контрольную ломаную 6 раз, а кривую 4 раза.

Дата добавления: 2015-10-29