Влияние Множественных УзлоFF

Множественные узлы значительно влияют на вычисление базисных функций и некоторых "счетных" свойств. Мы рассмотрим два из них, а на следующей странице будет пример расчета.

1. Каждый узел множественности k уменьшает ненулевой интервал самое большее k -1 базисных функций.
   Возьмем N_i,p (u) и N_{i +1, p} (u). Последнее не равно нулю на [ u_i, u_{i+p +1}) тогда как первое не равно нулю на [ u_{i +1}, u_{i+p +2}). Если сместить u_{i+p +2} до u_{i+p +1}, они станут двойным узлом. Тогда у N_i,p (u) будет по прежнему p +1 узловых интервалов, на которых она не равна нулю; но число узловых интервалов, на которых N_{i +1, p} (u) не равно нулю, уменьшается на 1, так как интервал [ u_{i+p +1}, u_{i+p +2}) пропадает.

Это наблюение можно легко обобщить. Фактически, не обращая внимания на изменение крайних точек узловых интервалов, создание узла множественности k влияет на k -1 базисных функций. Одна из них теряет один узловой интервал, вторая теряет два, третья - три, и так далее.

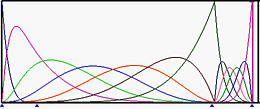
Выше показаны базисные функции 5 степени, где левый и правый крайние узлы имеют множественность 6, а все промежуточные узлы - простые (слева в верхнем ряду). Верхний рисунок справа - это результат смещения u ₅ до u ₆. Базисные функции, оканчивающиеся в u ₆, имеют меньше узловых интервалов, на которых они являются ненулевыми. На рисунках в среднем ряду u ₄, а затем u ₃ смещаются в u ₆, делая u ₆ узлом множественности 4. Нижний рисунок показывает результат после смещения u ₂ до u ₆, получаем узел множественности 5.

1. В каждом внутреннем узле множественности k, количество ненулевых базисных функций не больше p - k + 1, где p - это степень базисных функций.
   Так как смещение u_{i -1} в u_i растянет базисную функцию, ненулевая часть которой оканчивается в u_{i -1}, до u_i, это уменьшит количество ненулевых функций в u_i на одну. Точнее, увеличение множественности u_i на единицу уменьшает количество ненулевых базисных функций на единицу. Так как самое большее p +1 базисных функций могут быть ненулевыми в u_i, то количество ненулевых базисных функций в узле множественности k не больше (p + 1) - k = p - k + 1.

На рисунках выше, так как множественность узла u ₆ равна 1 (простой узел), 2, 3, 4 и 5, количества ненулевых базисных функций в u ₆ равны 5, 4, 3, 2 и 1.

Дата добавления: 2015-10-29