Некоторые Полезные Следствия Свойства Сильного Ограничивающего Многоугольника

Вспомним из свойства сильного ограничивающего многоугольника, что, если u лежит на [ u_i, u_{i +1}), то p (u) лежит в ограничивающем многоугольнике, описываемом контр. точками p _i, p _{i -1},..., p _{i-p +1}, p _i-p. Это поможет нам решить следующие задачи в проектировании кривых:

1. Сделаем криволинейный отрезок отрезком прямой: пусть p +1 контр. точек будут коллинеарными
   Если u лежит на узлово интервале [ u_i, u_{i +1}), то p (u) лежит внутри ограничивающего многоугольника для p +1 контрольных точек p _i, p _{i -1},..., p _{i-p +1}, p _i-p. Так как это верно для всех u на этом интервале, то отрезок кривой, находящийся на этом узловом интервале, лежит целиком в этом оганичивающем многоугольнике. Все эти p +1 контрольных точек являются коллинеарными (т.e. лежат на одной прямой), ограничивающий многоугольник вырождается в отрезок прямой, то же самое. происходит и с содержащимся в нем отрезком кривой. В итоге, отрезок кривой на узловом интервале [ u_i, u_{i +1}) становится отрезком прямой. Заметьте, что в этом случае отрезком прямой становится только этот отрезок кривой. Остальные отрезки остаются криволинейными.

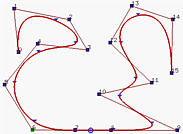
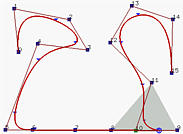
А вот вам и пример. На рисунках изображены кривые, для которых n = 15 (т.e. 16 контр. точек), p = 3 (степень равна 3), а m = 19 (т.e. 20 узлов). Заметьте, что первые четыре и последние четыре фиксированы. На рисунке слева в верхнем ряду исходная кривая. Давайте-ка сделаем p ₉, p ₈, p ₇ и p ₆ колинеарными. Таким образом, отрезок кривой [ u ₉, u ₁₀) лежит внутри огр. многоугольника точек p ₉, p ₈, p ₇ и p ₆. Так как этот многоугольник является отрезком прямой, то криволинейный отрезок также становится линейным. Но надо помнить, что первые четыре узла фиксированы и поэтому первых трех узловых интервалов нет. Так как [ u ₉, u ₁₀) - это седмой узловой интервал, седьмой сегмент вырождается в отрезок прямой p ₇ p ₈. Это показано на втором, третьем и четвертом рисунках.

Но почему вырождается только отрезок кривой на [ u ₉, u ₁₀)? Взгляните на второй рисунок. Темная область - это огранич. многоугольник прямо перед вхождением u в [ u ₉, u ₁₀). Этот огранич. многоугольник образуется точками p ₈, p ₇, p ₆ и p ₅, и еще не является отрезком прямой. Как только u входит в [ u ₉, u ₁₀), отрезок кривой вырождается (третий рисунок). Сразу после того, как u выходит из [ u ₉, u ₁₀), появляется новый огранич. многоугольник (четвертый рисунок).

На пятом рисунке p ₅ коллинеарна со следующими за ней четырьмя точками. На этой кривой еще один линейный отрезок. На шестом рисунке p ₁₀ коллинеарна с предшествующими ей пятью точками; тем не менее, она перемещена в положение между p ₈ и p ₉. Это должно сделать часть соответствующего отрезка кривой линейным (почему?)

1. Сделаем так, чтобы кривая B-spline проходила через контрольную точку: пусть p смежных контрольных точек будут одинаковыми
   Возьмем контр. точку p _i. Так как отрезок кривой на узловом интервале [ u_i, u_{i +1}) лежит целиком внутри огранич. многоугольника точек p _i,..., p _{i-p +1}, p _i-p, то, если сделать первые p контр. точек одинаковыми (т.e. p _i = p _{i -1} =... = p _{i-p +1}), то огр. многоугольник сожмется до отрезка прямой p _i-p p _i, а кривая должна будет пройти через точку p _i.

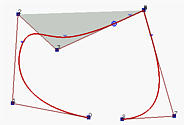
Степень кривой на левом рисунке равна 3. Если p ₅ переместить и сделать одинаковой с p ₆, кривая сместится ближе к p ₆, но все же не пройдет через нее. Это показано на среднем рисунке. Заметьте, что количество отрезков кривой от этого перемещения не изменяется; тем не менее, маленькая треугольная отметка рядом с p ₅ двигается ближе к p ₆.

Если p ₄ сместить и сделать одинаковой с p ₆ = p ₅, кривая пройдет через p ₆, а точка, соответствующая узлу, станет идентичной контрольной точке p ₄ из-за этого перемещения.

1. Сделаем кривую B-spline касательной сегменту контрольной ломаной: пусть p _i-p, p _{i-p +1} = p _{i-p +2} =.... = p _{i -1} = p _i и p _{i +1} будут коллинеарны
   Здесь p контр. точек делаются одинаковыми. В этой контрольной точке непрерывность C ⁰, потому что кривая имеет точку перегиба (или пересечения? блин) (смотри правый рисунок). Тем не менее, когда все узлы простые, кривая является C^{p -1}-непрерывной в узлах и бесконечно дифференцируемой в остальных местах, поэтому она является C^{p -1}-непрерывной в контрольнйо точке p _i (сжатая контр. точка, перенумерованная в i) на сегменте p _i-p p _i, а также C^{p -1}-непрерывной в контрольной точке p _i на сегменте p _i p _{i +1}. Таким образом, если сделать контр. точки p _i-p, p _i и p _{i +1} колинеарными, то из-за того, что два смежных отрезка кривой не имеют точки перегиба в узле, они будут C^{p -1}-непрерывными в p _i.

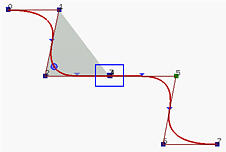
На рисунках выше - кривые 2 степени. Если сделать контр. точки 2, 3, 4 и 5 колинеарными, а 3 и 4 совместить, получим правый рисунок. Колинеарность делает отрезок кривой лежащим на прямой, а совмещенные контр. точки дают C ^3-1 = C ²-непрерывность.

Дата добавления: 2015-10-29