В) Вычисление интервала корреляции;

Интервал корреляции – такая величина, при котором еще сохраняется статистическая связь между значениями случайного процесса.

(4.5)

Чтобы вычислить 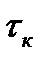, необходимо вычислить B(0). По графику (4.2) видим, что . Преобразовав функцию корреляции используя алгебраические, тригонометрические преобразования и свойство первого замечательного предела при 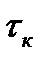проверим графический метод:

Интеграл 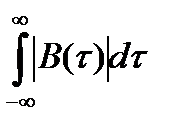не удалось вычислить ни в ручную, ни пакетами программ Mathcad 14, MathLab 7.0, Advanced Grapher, SMathStudio, которые хоть и помогли, но результаты получались совершенно неприемлемые.

Попробуем вычислить графическим путем, используя свойство (4.6) и инструмент «трассировка» по графику в математических пакетах Mathcad 14 и Advanced Grapher.

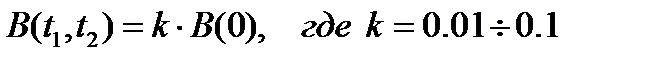(4.6)

Возьмем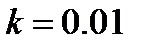

По графику смотрим чему равно на первой положительной «полуволне»

Рис 4.3 Корреляционная функция случайного сигнала в увеличенном виде и окно трассировки.

Видим, что значение t_k при B(t_k)=1.6 равно: t_k≈6.34 ∙ 10^-4 c

Произведение эффективной ширины спектра и интервала корреляции должно равняться p. Формула (4.7)

t_k≈6.34 ∙ 10^-4 c

(5.9)

Подставим:

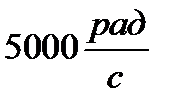6.34 ∙ 10^-4 c = 3.17 ≈ π

Условие (5.9) выполняется.

Нелинейное преобразование сигналов.

Требуется определить плотность распределения вероятностей w (y) процесса на выходе цепи y (t), его математическое ожидание, дисперсию и среднеквадратическое отклонение.

Стационарный гауссовский случайный процесс u (t) с заданными параметрами m (t) и s (t) воздействует на безынерционную нелинейную цепь с характеристикой:

y= a ₂ × x² при -∞ < x < ∞, a ₂=1

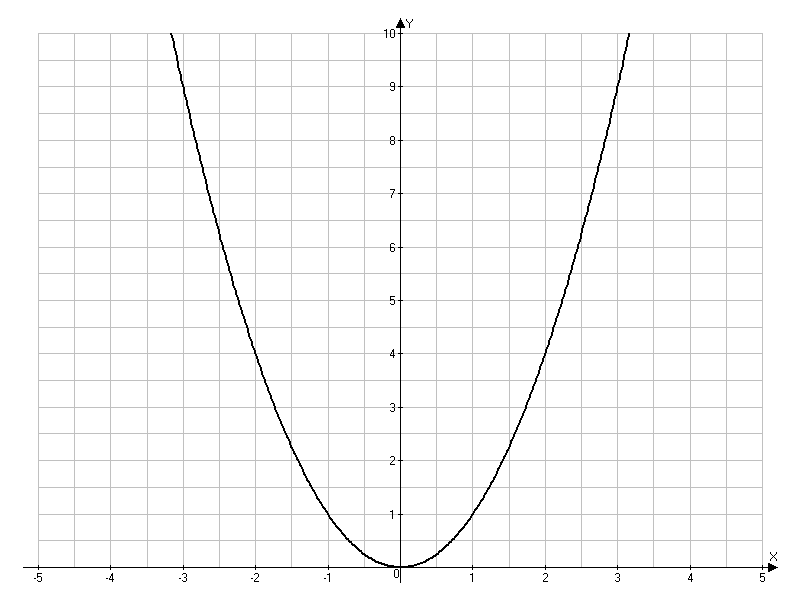
Рис 5.1 Характеристика безынерционного нелинейного устройства

Дан стационарный гауссовский случайный процесс u(t) с параметрами и .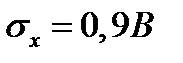

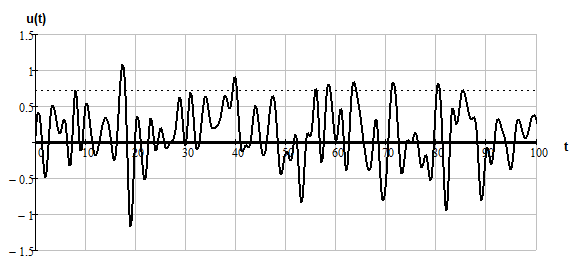
Рис 5.2 Стационарный гауссовский случайный процесс u(t)

Плотность распределения вероятности процесса на выходе нелинейной безынерционной цепи (НБЦ ) связан с плотностью распределения процесса на входе следующим выражением:

(5.1)

Найдем обратную функцию, ее производную и подставим в формулу(5.1):

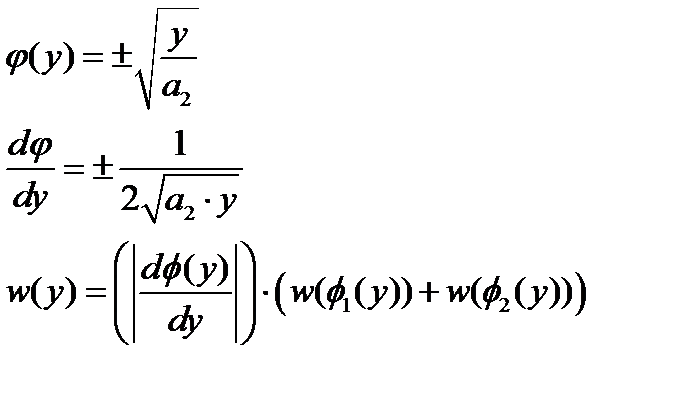
Последнее выражение получилось потому, что функция неоднозначна.

Так как процесс на входе нелинейной безынерционной цепи является гауссовским случайным процессом с математическим ожиданием равным нулю (по условию m_x(t) = 0 B) (5.2), то его плотность распределения вероятностей определяется по следующей формуле:

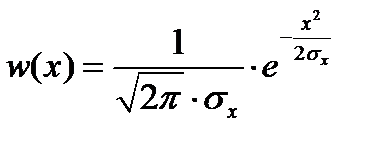(5.2)

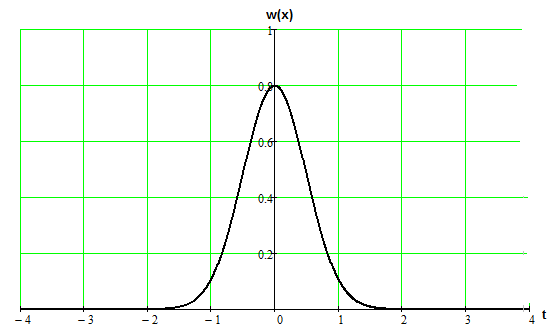
Рис 5.3 Плотность вероятности случайного процесса с заданными

Дата добавления: 2015-10-26