В) Нахождение математического ожидания, дисперсии и среднеквадратическое отклонения.

Нахождение математического ожидания, дисперсии и среднеквадратическое отклонения усреднением по множеству реализаций:

(3.5)

D = -(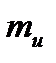)² (3.6)

σ = (3.7)

По формулам (3.5), (3.6), (3.7) а так же свойству (3.3) вычисляем математическое ожидание, дисперсию и среднеквадратическое отклонение.

D= ²-(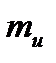)²=0.238-0²=0.238 В

σ = = = 0.488 В

Нахождение математического ожидания, дисперсии и среднеквадратическое отклонения усреднением по времени (процесс по условию эргодический):

(3.8)

(3.9)

σ = (3.10)

По формулам (3.8), (3.9), (3.10) вычисляем математическое ожидание, дисперсию и среднеквадратическое отклонение.

T_u=T₁+T₂=1+0.4=1.4

Функцию U(t) от 0 до T₁ (прямая линия) найдем из уравнения прямой, проходящей через две точки: (u-u₁)/(u₂- u₁)= (t-t₁)/(t₂- t₁), где (u₁, t₁) и (u₂, t₂) координаты точек, соответственно равные (-1,0) и (1,1) см. рис 3.2

Отсюда U(t)=2t-1 от 0 до T₁

U(t)=0 от T₁ до T₂

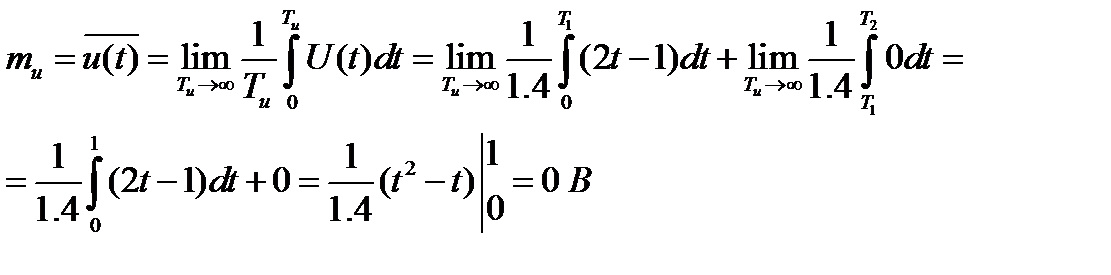
σ = = = 0.488 В

Напомним физический смысл математического ожидания, дисперсии и среднеквадратическое отклонения:

Математическое ожидание представляет собой среднее значение случайного процесса в текущий момент времени t. В нашем случае математическое ожидание равно нулю (реализации группируются по обе стороны от оси времени). Такой процесс называется центрированный. Физический смысл величины постоянная составляющая U.

Дисперсия характеризует разброс мгновенных значений реализаций случайного процесса относительно его среднего значения. Физический смысл мощность переменного составляющего случайного процесса.

Физический смысл среднеквадратическое отклонения – действующие значения напряжения или тока на единичном сопротивлении.

Рис 3.4 Математическое ожидание, дисперсия и среднеквадратическое отклонение на реализации сигнала и его плотности распределения вероятности

г) Определение вероятности того, что значения сигнала будут находиться в заданном интервале от U ₁до U ₂.

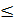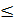Вероятность попадания значений сигнала в заданный интервал U₁ U U₂

определяется через плотность распределения вероятности известным соотношением:

По условию -0.5В 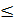U 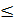0.2В. По формуле (3.11) определяем вероятность:

Рис 3.5 Вероятность того, что значения сигнала будут находиться в заданном интервале от U ₁до U ₂

Дата добавления: 2015-10-26