Вычисление дисперсии иа основании индивидуальных значений испытуемых

X	d	d^1
индивидуальные значения	отклонения от средних	квадрат отклонений
	-5
	-3
	I
II
х=6		Zd^2=61
среднее		сумма
		квадратов

В своей книге „Социальная физика" (1835), Кетле показал, что час­тотные распределения самых различных характеристик, будучи пред­ставленными графически, образуют нормальное распределение. Из это­го он сделал вывод, что природа в создании человека стремится к сред­ним величинам. Однако иногда ей не удается достичь своей цели - она „промахивается". Небольшие ошибки (соответствующие небольшим отклонениям) встречаются чаще, а большие - крайне редко.

Идея Кетле о нормальном распределении была положена Гальто-ном в основу его рассуждений о наследственной обусловленности спо­собностей человека. Способности, как считает Гальтон, также имеют нормальное распределение: больше всего существует людей со средним уровнем умственного развития, а гении и полные бездарности встреча-' ются крайне редко. Именно для подтверждения этого положения Галь­тон и проводил психологические эксперименты на многотысячных выборках испытуемых.

Однако в отличие от Кетле, который пытался объяснить „ошибки" природы с точки зрения теории вероятности - теории, имеющей уже двухвековую историю к моменту появления его книги, - Гальтон видел причину нормального распределения способностей в их наследствен­ной обусловленности.

Разделяя представления Дарвина о том, что эволюция осуществля­ется путем естественного отбора, Гальтон приложил основные положе­ния этой теории к объяснению источников различий в способностях человека...

Теория Дарвина базируется на трех принципах - на принципе из­менчивости (согласно которому по многим характеристикам существу­ют большие индивидуальные различия или межиндивидуальная измен­чивость), на принципе наследственности (заключающемся в том, что дети похожи на родителей больше, чем на тех, кто не связан с ними родственными узами) и на принципе отбора (состоящем в том, что более приспособленные имеют больше шансов выжить и оставить потомство).

Различия между людьми по способностям очевидны (принцип из­менчивости). Генеалогический анализ родственников великих людей позволил Гальтону сказать о наследственной передаче способностей (принцип наследуемости). Объединение этих положений привело его к мысли о наследственной обусловленности межиндивидуальной измен­чивости, т.е.индивидуальных различий. А раз так, то, следовательно, общество должно все свои силы направить на помощь наиболее талан­тливым людям: это повысит их приспособленность и, в результате, из­менит в лучшую сторону весь человеческий вид (принцип отбора).

Представления Кетле о закономерностях, приложимых к индивиду­альным различиям, были развиты статистиками К. Пирсоном и Р. Фи­шером. Они же создали методы, позволяющие оценить соотношения

между различными характеристиками. Появление первого такого ме­тода - корреляционного анализа - непосредственно связано с именем Гальтона (Пирсон был его учеником и коллегой) и с логикой развития его исследований, требующих создания более точных оценок степени сходства родителей и детей.

Показатель, получаемый при использовании корреляционного ана­лиза, - коэффициент корреляции - является мерой связи между двумя характеристиками и свидетельствует о том, в какой степени изменчи­вость одной из рассматриваемых характеристик сопровождается, в сред­нем, изменчивостью другой. Величины коэффициентов корреляции могут меняться в пределах от -1 до 1, при этом, чем дальше значение коэффициента от 0, тем более тесной является связь между характерис­тиками. Способы вычисления различных типов корреляций можно на­йти в любом учебники по статистике (например, Дж. Гласе, Дж. Стэн­ли, 1976). Здесь же будет на примере рассмотрен смысл коэффициента корреляции.

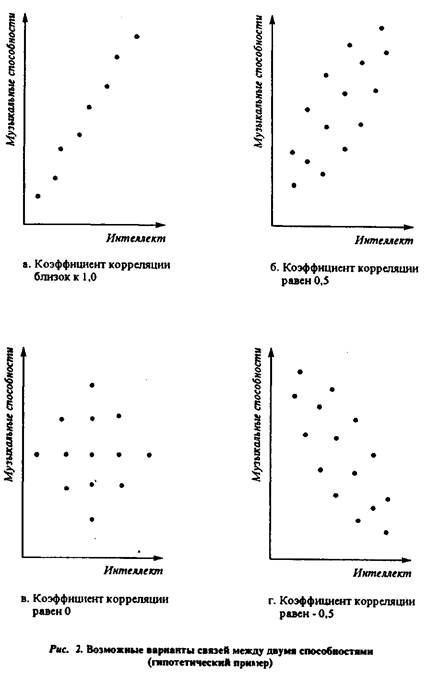
Допустим, нам необходимо выяснить, связаны ли, и если связаны, то в какой степени, особенности интеллектуального развития ребенка и его музыкальные способности. Построим график (см. рис. 2), у кото­рого одна ось представляет собой показатели интеллекта (например, баллы по тесту интеллекта), а другая - показатели музыкальных спо­собностей (например, экспертные оценки учителя музыки). Точками отметим индивидуальные значения испытуемых. Местоположение каж­дой точки определяется уровнем развития интеллекта данного ребенка (абсцисса) и уровнем его музыкальных способностей (ордината). На­неся на график индивидуальные значения всех своих испытуемых, мы можем получить разные картины.

Если распределение точек окажется таким, как на рисунке 2а или 26, можно говорить, о том, что связь между этими характеристиками существует и эта связь - положительная, т.е. чем выше у ребенка одни способности, тем выше и другие. Однако взаимообусловленность свя­зей в двух этих, случаях различна. В первом случае (2а) связь тесная, и коэффициент корреляции вычисленный на основании таких данных будет приближаться к 1. Во втором случае (26) связь существует, но коэффициент корреляции не слишком высок - примерно 0,5.

Картина, полученная на рисунке 2в, свидетельствует об отсутствии взаимосвязей. Нет основания для вывода, что более музыкальные дети одновременно являются и более развитыми интеллектуально. Коэффи­циент корреляции равен в этом случае 0.

На рисунке 2г показан пример отрицательной связи, т.е. чем выше интеллект ребенка, тем ниже его музыкальные способности.

Коэффициент корреляции указывает на два факта: во-первых, есть ли связь между параметрами и, во-вторых, если связь есть, то насколь­ко она тесная.

Связь между параметрами есть, если коэффициент корреляции ока­зывается значимым, т.е., если есть высокая степень вероятности того, что полученная закономерность верна для большинства случаев. Зна­чимость коэффициентов корреляции вычисляется по таблицам, кото­рые содержатся в большинстве статистических справочников и учеб­ников на основании величины коэффициента корреляции и количест­ва испытуемых. Чем больше испытуемых, тем меньшая величина коэф­фициента корреляции окажется значимой.

На тесноту связи указывает величина коэффициента корреляции. Чем дальше эта величина от 0 и ближе к 1 или к -1, тем связь более тесная (рис.2).

Допустим, проведя эксперимент, мы получили значимый коэффи­циент корреляции, равный 0,5. Как можно проинтерпретировать этот результат? Мы можем сказать, что связь есть, но она не очень тесная. Иначе говоря, в среднем, дети с высоким уровнем интеллекта будут иметь одновременно и хорошие музыкальные способности, но при срав­нении двух случайно взятых из выборки детей мы всегда можем стол­кнуться с тем, что ребенок с более высоким интеллектом будет иметь более низкие музыкальные способности. Чем ближе коэффициент кор­реляции к 1 или к -1, тем меньше вероятность найти такую пару детей. Однако, поскольку обычно приходится иметь дело со средними вели­чинами корреляции, необходимо помнить, что закономерности, полу­ченные на группе нельзя переносить на отдельных конкретных людей.

Такая связь, как описанная в нашем гипотетическом примере, мо­жет быть результатом самых разных взаимоотношений между интел­лектом и музыкальными способностями. Во-первых, связь между ними может быть результатом какого-то третьего влияния (например, у тех детей, с которыми постоянно занимаются родители, оказывается выше и уровень развития, и успехи в музыкальной школе). Во-вторых, одна из этих способностей может влиять на другую и повышать ее. В-треть­их, есть некоторая вероятность того, что обнаруженная связь не отра­жает содержательной общности между этими двумя характеристика­ми, а является артефактом. (Как остроумно заметил американский воз­растной психолог Дж Кэган, если измерять каждый год расстояние от земли до кометы Галея и цены на нефть, то между ними будет обнару­жена высокая корреляция. Но это не означает, что одно определяет другое, или что оба являются следствием какой-то третьей причины. Просто обе эти характеристики имеют тенденцию монотонно убывать. Это и определяет связь между ними).

Как становится понятным из всего здесь сказанного, оценить меру связи между различными характеристиками возможно только в том слу­чае, если каждая из этих характеристик имеет разброс значений, т.е. если каждая из них по-разному проявляется у разных людей. Корреля­ции между характеристиками, не имеющими разброса (например,

между количеством ног и количеством рук у здоровых людей), бу­дут равны 0.'.•••••;. -i»:;.:,;.- -.:• '-,:-•.'-:. у.-,-..,:..о::;'?:' Ч '-С..?-,:

Исследование взаимосвязей между разными психологическими ха­рактеристиками и исследование структур этих характеристик не толь­ко в период зарождения психологии индивидуальных различий, но и в дальнейшем демонстрируют ее тесную связь со статистикой? Наиболее ярким примером этого является изменение представлений о'структуре психологических свойств, произошедшее, благодаря появлению фак­торного анализа -метода группировки взаимосвязанных характерис­тик. Автор'^факторнЪ-аналитического подхода ^гк исследованию личности, Раймонд Кэттел, одновременно является и создателем ряда техник факторного анализа. Подробно это будет-обсуждаться во II

ЧаСТИ КНИГИ. ^: ^ >.'.-• ^г.-- -^ ••'.•'• '..•' *?'.»: ^.bi;.'?: 'гчког?;г,м; t^' s

Дата добавления: 2015-10-23