Соотношение между корреляционной и факторной матрицами (цит. по Buss A.R., Pbley W., 1976)

Таблица

Корреляционная матрица	Факторная матрица	Транспонированная факторная матрица
Черты	Черты
							А	В 1	2 3 4 5 6
		0.72	0.0	0.27	0.0	0,63	0,9	0,0 0.9	0.8 0.0 0.3 0,0 0.7
	0,72		0.16	0.40	0,12	0.56	0.8	0.2 0.0	0.2 0.8 0.8 0.6 0.0
	0.0	0.16		0.64	0.48	0.0	о.о	0.8
	0.27	0.40	0.64		0.48	0.21	0,3	0.8
	0.0	0.12	0.48	0.48		0.0	0.0	0,6
б	0.63	0.56	0.0	0.21	0.0		0.7	0.0
(Корреляционная матрица) =	(Факторная х матрица)	(Транспонированная факторная матрица)

Корреляционная матрица равна произведению факторной матри цы на транспонированную факторную матрицу. А каждый коэффици ент корреляции между двумя переменными равен факторному весу пер­вой переменной, умноженному на факторный вес второй переменной,

в первом факторе плюс факторному весу первой переменной, умножен­ному на факторный вес второй переменной, во втором факторе. На­пример, коэффициент корреляции между второй и четвертой перемен­ной равен:

(0,8 х 0,3) + (0,2 х 0,8) = 0,24 + 0,16 = 0,40.

В зависимости от разновидности применяемого факторного анали­за и от особенностей изучаемых черт на основе одной и той же корре­ляционной матрицы можно получить разное количество факторов. Если бы факторов было три, то коэффициент корреляции был бы равен сум­ме произведений факторных весов в первом, втором и третьем факто­ре. Каким бы ни было количество факторов, коэффициент корреляции между двумя переменными всегда равен сумме произведений весов во всех выделенных факторах.

Подведем некоторые итоги. Во-первых, факторный анализ позво­ляет сгруппировать исследуемые черты. Во-вторых, эта группировка производится на основании тех связей, которые есть между перемен­ными и приводит к выделению более общих психологических черт. В-третьих, в факторных весах отражаются те связи, которые существу­ют между чертами.

'Далее рассмотрим, как интерпретируются полученные факторы и как выясняется, каков смысл латентной переменной, определяющей корреляции между чертами. ^!

Есть два классических примера, демонстрирующих эмпирический смысл факторного анализа. Первый из них - это „коробка Терстона". Л. Терстон брал разные коробки и измерял у них все размеры, которые только можно придумать. Всего у каждой коробки он вычислял 26 по­казателей. Прокоррелировав эти показатели между собой и проведя факторный анализ на основе связей между различными показателями, он выделил 3 фактора - длину, ширину и высоту. Таким образом, 3 латентных переменных являются основными для всех других размеров, остальные - производными от этих трех.

Второй пример - „шар Кэттела". Р. Кэттелл не только измерял раз­личные шары, но и оценивал различные параметры их движения на наклонных плоскостях. В итоге факторизации полученных переменных он получил три фактора - размер, вес и эластичность.

Эти два примера показывают, что факторный анализ действитель­но позволяет выделить наиболее существенные черты.

Теперь рассмотрим, как производится интерпретация конкретных экспериментальных данных. Допустим, в эксперименте измерялось 4 черты. Название этих черт и факторная матрица, полученная после факторизации результатов, представлены в таблице 8.

В первом факторе наибольшие факторные веса имеют первые две черты, Связанные со скоростью решения задач (0,9 и 0,8). На этом осно­вании мы можем заключить, что содержание первого фактора опреде-

tt-

ляется скоростными характеристиками деятельности. Во втором фак­торе наибольшие веса имеют показатели тех заданий, успешность вы­полнения которых связана с памятью (0,8 и 0,7). Следовательно, содер-, жание второго фактора связано с памятью. Таким образом, скорость,' деятельности и память являются теми характеристиками, которые оп­ределяют взаимосвязи между.четырьмя исследовавшимися переменны­ми. Скорость и память представляют собой более общие черты по от; ношению к четырем более.частным (тестовым показателям)..',j.^'.j,,..'_£ |

'»;.',':f:

Факторная структура четырех переменных., *\ (гипотетический пример)

Таблица'8

Черта	Фактор 1 • •	Л Фактор 2 •,
Скорость решения задач ^:<Скорость сложений фигур Повторение цифр Повторение предложений	' 0,9 '-" ,?:•.' 0,8 •'»•'•- ^;'--.: 0,2 ( ;. 0,4	'.'-• 0,1 ''•',"' •••-. ' - 0,3: i-i.,0,8,.' 0,7.

К сожалению, не всегда различия между факторными весами ока­зываются столь чёткими, как в приведенном примере. Если разница между факторными весами разных переменных.небольшая,то фактор интерпретировать невозможно. В этом случае проводится специальная процедура, которая называется вращением (ротацией). Что вращается и к чему это в результате приводит, продемонстрируем на примере.

• т Допустим, в результате статистической обработки результатов, была получена такая факторная матрица, как показано на рисунке 8 (а). Ин­терпретировать эти результаты невозможно: факторные, веса всех пе­ременных оказываются близкими по значению.,Однако можно изме­нить способ получения данных. Для того,.чтобы понять, как, это де­лается представим полученные результаты в.графической,форме

(см*, рис.8 (в)). •" " '..,;;;.,..:,..::^г;.,, -I ' _;f...''"..'.,:,',,";.'!

- Каждую исследовавшуюся черту можно представить как точку в двумерном:пространстве. Оси этого, пространства образуют,факторы А и В, а проекции каждой точки на эти оси являются.факторными веса-! ми. Так, проекция! точки 1 на ось А равна 0,6, а на ось В-равна 0,4J; Повернем фактор'ные оси таким образом, чтобы проекции на них од-> них показателей стали - близки к 0, а проекции, других показателей, -приблизились к 1 /В данном случае,такая цель,будет,достигнута при

-повороте осей на 50 градусов^Тсперь проекции трчки^,на факторные оси А и В будут р;1вны 0,08 #0,72, а новая факторная матрица, (после вращения) будет такой, как показано на рисунке 8(6). Интерпретирр-

'.'вать'содержание факторов в новой матрице уже-значительно легче,

••поскольку:в каждом факторе есть черты с большими факторными ве­сами и есть черты с низкими факторными весами.,, 1.'.'.',' _м,.,.

а),.

Факторная матрица до вращения -

. •, б) '.

Факторная матрица после.вращения '

• Черты ' '•.-••..,! -Л Г	Факторы
А	В
' *.'•	1 ^i:iV .2-.:f.,%, 3 4	•0.6' 0.6 0.7 0.4	0.4 0.6 •0.3 •0.5
' Черты'- Л •->;.: --М;'. *	Факторы
А^1	<ti
, -,..;,,: -, •-, -,- • 2 ••'•••"• • -• Зл- '• 4	0,08 •0.07 0.68 0,64	0.72 0.85 0.34 •0.02

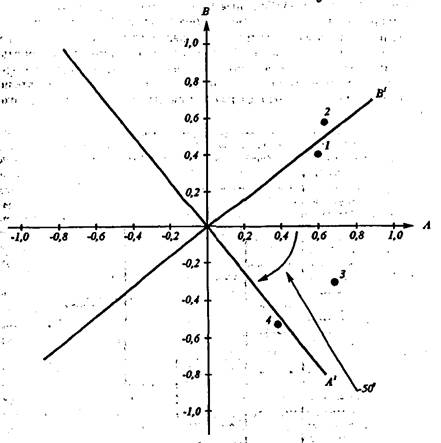
Рис. 8. Факторные матрицы до и после крашения и геометрическое изображение процедуры вращения факторных осей (цнт. no Buss AJL, Poley W₄ 1976)

В примере, показанном на рисунке 8(в), факторные оси и до, и после вращения находятся под прямым углом друг к другу, т.е процедура факторизации построена таким образом, чтобы получить не коррели­рующие друг с другом факторы (ортогональные факторы). если при вращении изменить не только положение осей, как это было сделано в нашем примере, но и изменить угол между осями (поставить оси не под прямым углом друг к другу), то полученные факторы будут коррели­ровать друг с другом. Такое вращение, при котором факторные оси пересекаются не под прямым углом, называется облическим вращени­ем. Поскольку между факторами при облическом вращении будет кор­реляция, то их опять можно факторизовать, получив „факторы факто­ров" или факторы второго порядка. Вторичные факторы представля­ют собой еще более обобщенные черты, чем первичные. При обли­ческом вращении факторов второго порядка их опять можно фактори­зовать и получить факторы третьего порядка и т.д.

Таким образом, на основе облического вращения можно построить иерархию черт: тестовые показатели —> факторы первого порядка—> факторы второго порядка —> и т.д. (см. рис. 9). Тестовые показатели представляют собой множество разнообразных черт, факторы первого

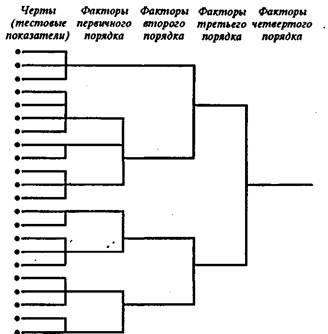
Рис. 9. Иерархическая структура факторов

порядка группируют эти черты и сводят их к меньшему числу показа­телей, факторы второго порядка позволяют найти то общее, что есть в этих группах, и сводят их к еще меньшему числу показателей.

Зная процедуру получения факторов, можно понять, что факторы, полученные на основе психологических черт (например, тестовых по­казателей) представляют собой не сумму и не квинтэссенцию всего того, что есть в отдельных чертах, а базовую характеристику по отношению к отдельным чертам. Чем более высок порядок фактора, тем более обоб­щенной характеристикой психической деятельности он является и тем в меньшей степени в нем представлена специфика отдельных психоло­гических черт.

В современной психологии факторный анализ широко использует­ся при изучении самых разных психологических явлений и применяет­ся для выделения психологических черт и для выяснения соотношения между различными чертами.

Дата добавления: 2015-10-23