Векторное произведение двух векторов. Условие коллинеарности векторов. Вычисление площади параллелограмма и треугольника.

Векторным произведением вектора на вектор называется третий вектор который обладает следующими свойствами:

1. Его длина равна =

2. Вектор перпендикулярен к плоскости, в которой лежат вектора и

3. Вектор направлен так, что поворот от вектора к вектору осуществляется против часовой стрелки, если смотреть из конца вектора (в этом случае, говорят, что тройка векторов и – правая).

Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.

a={a_x; a_y; a_z} и b={b_x; b_y; b_z} коллинеарны если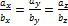

Геометрический смысл векторного произведения: модуль векторного произведения векторов численно равен площади параллелограмма или удвоенной площади треугольника, построенных на этих векторах как на сторонах.

Свойства векторного умножения. Векторные произведения координатных ортов.

Основные свойства векторного произведения:

антикоммутативность:

;

однородность:

;

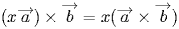дистрибутивность:

.

Векторное произведение ортов

i × j=k, j × i= −k,
j × k=i, k × j= −i,
k × i=j, i × k= −j.

Векторное произведение двух векторов в координатной форме.

12. Смешанное произведение трех векторов. Условие компланарности векторов. Объём параллелепипеда и тетраэдра.

Смешанное произведение векторов a, b, c — скалярное произведение вектора a на векторное произведение векторов b и c.

Векторы называются компланарными, если существует плоскость, которой они параллельны.

Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда или шести объёмам тетрайдера, образованных векторами a, b, c.

Смешанное произведение трех векторов в координатной форме. Свойства смешанного произведения.

Свойства

1) перестановка любых двух сомножителей меняет знак произведения, т.е.: (a, b, c) = - (b, a, c) = (b, c, a) = - (c, b, a) = (c, a, b) = - (a, c, b)

2) если смешанное произведение равно нулю ((a, b, c) = 0), то векторы a, b, c - компланарны

Дата добавления: 2015-10-24