
Читайте также:
|
Длина векторного произведения:  , где , где  . .
 , где , где 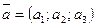 , , 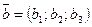 . .
|
Задание 20. Даны векторы  и и  . Вычислите: . Вычислите:
| |||||||||||||||||||||
а) 
| |||||||||||||||||||||
b) 
| |||||||||||||||||||||
с) 
| |||||||||||||||||||||
Ответ: а) (-8; -1; 5), b) (40; 5; -25), c) (48; 6; -30).
Геометрический смысл векторного произведения

|
Задание 21. Найти площадь параллелограмма, построенного на векторах  и и  . .
| |||||||||||||||||||||||||||||||||
Ответ:  .
.
Задание 22. Найти площадь параллелограмма, построенного на векторах  и и  , если , если  , , 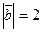 и и  . .
| ||||||||||||||||||||||||||||||||||
Ответ:  .
.
Площадь треугольника
 . .
|
Задание 23. На векторах  и и 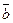 построен треугольник. Найдите его площадь, если построен треугольник. Найдите его площадь, если  , , 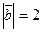 , ,  . .
| |||||||||||||||||||||||||||||||||
Ответ:  .
.
Задание 24. Даны:  , , 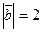 , ,  . Вычислить площадь параллелограмма, построенного на этих векторах. . Вычислить площадь параллелограмма, построенного на этих векторах.
| |||||||||||||||||||||||||||||||||
Ответ:  .
.
| Задание 25. В треугольнике с вершинами А(1; -1; 2), В(5; -6; 2), С(1; 3; -1) найти высоту BD. | |||||||||||||||||||||||||||||||||
Ответ:  .
.
Смешанное произведение векторов
Смешанное произведение векторов 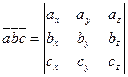 . .
|
Условие компланарности векторов
  векторы векторы  компланарны. компланарны.
|
Задание 26. Проверить, компланарны ли векторы  , ,  , ,  . .
| |||||||||||||||||||||||||||||||||
Ответ: компланарны.
Задание 27. Даны векторы  , , 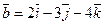 , , 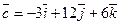 . При каком . При каком 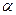 эти векторы компланарны? эти векторы компланарны?
| |||||||||||||||||||||||||||||||||
Ответ:  .
.
| Задание 28. Показать, что точки А(2; -1; -2), В(1; 2; 1), С(2; 3; 0), D(5; 0; -6) лежат в одной плоскости. | |||||||||||||||||||||||||||||||||
Геометрический смысл смешанного произведения
 . .
|
Задание 29. Найдите объем параллелепипеда, построенного на векторах:  , , 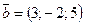 , , 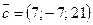 . .
| |||||||||||||||||||||||||||||||||
Ответ: 49.
Объем пирамиды
 . .
|
| Задание 30. Построить пирамиду с вершинами D(-5; 2; -4), А(-4; 2; 6), В(2; -3; 0), С(-10; 5; 8) и вычислить ее объем и высоту пирамиды, опущенную на грань АВС. | |||||||||||||||||||||||||||||||||
Ответ: 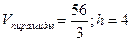 .
.
Аналитическая геометрия. Основные понятия
Дата добавления: 2015-10-29; просмотров: 114 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Скалярное произведение векторов | | | Прямая на плоскости 1 страница |