
Читайте также:
|
Векторная алгебра. Основные понятия
Линейные операции над векторами
Задание 1.
а) 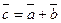 соответствует рисунку № соответствует рисунку №
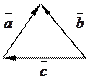     1) 2) 3) 4) 5)
Ответ: 1) 2) 3) 4) 5)
Ответ:
|
b)  соответствует рисунку № соответствует рисунку №
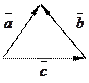    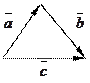 1) 2) 3) 4) 5)
Ответ: 1) 2) 3) 4) 5)
Ответ:
|
c) 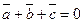 соответствует рисунку № соответствует рисунку №
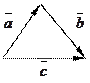  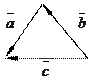 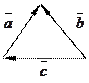  1) 2) 3) 4) 5)
Ответ: 1) 2) 3) 4) 5)
Ответ:
|
 Задание 2. Какой вектор рисунка отвечает следующим векторам:
a) Задание 2. Какой вектор рисунка отвечает следующим векторам:
a)  b)
b)  c)
c) 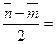

|
Задание вектора через координаты в декартовой системе координат
На плоскости вектор определяется следующим образом:  
| В пространстве вектор определяется следующим образом:  
|
Длина вектора  . .
| Длина вектора  . .
|
Координаты вектора
  ,
где
т. ,
где
т.  - начало вектора,
т. - начало вектора,
т.  - конец вектора. - конец вектора.
| Координаты вектора
  ,
где
т. ,
где
т.  - начало вектора,
т. - начало вектора,
т.  - конец вектора. - конец вектора.
|
| При сложении векторов их соответствующие координаты складываются, а при умножении вектора на число умножаются на это число и его координаты. |
Задание 3. В декартовой системе координат заданы координаты вершин треугольника  : :  , ,  , , 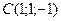 . Найти координаты векторов . Найти координаты векторов  , , 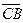 , ,  и координаты вектора и координаты вектора 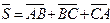 . .
| |||||||||||||||||||||||||||||||||
Определение орта вектора
Единичный вектор, направление которого совпадает с направлением вектора  , называется ортом вектора , называется ортом вектора  и обозначается и обозначается 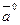 : : 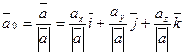
 , где , где  - углы, которые вектор составляет с координатными осями; - углы, которые вектор составляет с координатными осями; 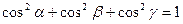 . .
|
Задание 4. Вектор  составляет с осями составляет с осями  и и 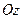 углы 600 и 1200. Найти его орт, если углы 600 и 1200. Найти его орт, если  - острый. - острый.
| |||||||||||||||||||||||||||||||||
Ответ: 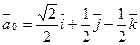
Задание 5. Найти длину вектора 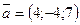 и координаты орта. и координаты орта.
| |||||||||||||||||||||||||||||||||
Ответ: 
Деление отрезка в данном отношении
Формулы для нахождения координат точки  , делящей в данном отношении , делящей в данном отношении  отрезок отрезок  имеют вид: имеют вид:  ; ;  . .
|
Задание 6. Точка М делит отрезок АВ в отношении  . Найти координаты точки М и точки В, если . Найти координаты точки М и точки В, если  , ,  . .
| |||||||||||||||||||||||||||||||||
Ответ: 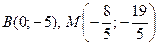 .
.
Условие коллинеарности векторов
Координаты коллинеарных векторов 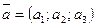 и и 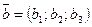 удовлетворяют соотношению: удовлетворяют соотношению:
 . .
|
Задание 7. Среди заданных векторов  , , 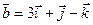 , , 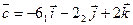 , , 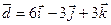 указать коллинеарные пары векторов. указать коллинеарные пары векторов.
| |||||||||||||||||||||||||||||||||
Скалярное произведение векторов
 , где , где  или или
 , где , где 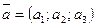 , , 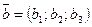
|
Задание 8. Найти  , если , если  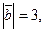 
| |||||||||||||||||||||||||||||||||
Ответ: 16
Задание 9. Найти длину вектора 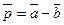 , если , если 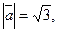 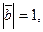 
| |||||||||||||||||||||||||||||||||
Ответ:  .
.
Задание 10. Даны векторы  и и  .
Вычислить: а) .
Вычислить: а)  ; b) ; b)  ; c) ; c) 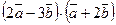 . .
| |||||||||||||||||||||||||||||||||
Ответ: а) 22; b) 6; c) -200.
Задание 11. Определить угол между векторами 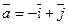 и и  . .
| ||||||||||||||||||||||||||||||||||
Ответ:1350
Задание 12. Найти вектор  , удовлетворяющий условиям: , удовлетворяющий условиям:  коллинеарен коллинеарен 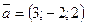 и и  . .
| |||||||||||||||||||||||||||||||||
Ответ:  .
.
Проекция вектора 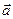
На ось 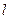 : :
 ,
где ,
где  угол между осью угол между осью 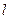 и вектором и вектором 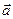 , отсчитываемый от оси , отсчитываемый от оси 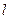 до до 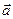 против часовой стрелки. против часовой стрелки.
| На вектор 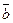 : :

|
Дата добавления: 2015-10-29; просмотров: 117 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тест по Маркетингу_2 | | | Векторное произведение векторов |