Теорема о пределе функции, заключенной между двумя функциями, имеющими один и тот же предел.

Если функция f(x) заключена между двумя функциями g(x) и p(x), имеющими один и тот же предел, то она стремится к этому же пределу.

Определение бесконечно малой функции. Теорема о сумме и произведении конечного числа бесконечно малых функций, а также о произведении бесконечно малой функции на ограниченную функцию.

Функция 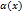называется бесконечно малой при 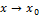, если

Сумма и произведение конечного числа бесконечно малой функции есть функция бесконечно малая.

Произведение бесконечно малой функции на ограниченную есть функция бесконечно малая.

9. Теорема о необходимом и достаточном условиях выполнения равенства с использованием понятия бесконечно малой функции. Бесконечно большие функции и их свойства.

Если f(x) имеет предел, то её можно представить как сумму постоянной и бесконечно малой функции.

Функция называется бесконечно большой при 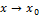, если предел этой функции

Сумма и произведение бесконечно больших функций есть функция бесконечно большая.

Сумма бесконечно большой функции и ограниченой есть функция бесконечно большая

Произведение бесконечно большой функции на есть функция бесконечно большая.

Правила сравнения бесконечно малых функций.

Допустим, у нас есть бесконечно малые при одном и том же величины и

Если , то 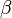— бесконечно малая высшего порядка малости, чем . Обозначают .

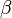Если , то — бесконечно малая низшего порядка малости, чем . Соответственно .

Если 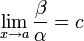(предел конечен и не равен 0), то и 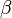являются бесконечно малыми величинами одного порядка малости.

Это обозначается как или (в силу симметричности данного отношения).

Если (предел конечен и не равен 0), то бесконечно малая величина 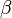имеет -й порядок малости относительно бесконечно малой .

Первый замечательный предел.

Предел отношения sinx к x при 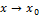равен 1.

Второй замечательный предел.

или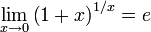

Дата добавления: 2015-10-24